0 引言

    前缘缝翼位于机翼前缘的上方，作用是在大迎角下改变翼型的相对弯度和吹除附面层以增加机翼的升力。左右机翼分别设置三段前缘缝翼，每段布置三根滑轨，各段互不相连。其可靠性与飞机的安全直接相关，一旦其收放机构出现故障，轻者飞机受损，重者机毁人亡。所以针对缝翼的收放动作，研究其运动过程中的动态响应和运动可靠性意义重大。但由于缝翼机构体积大、结构形式复杂，传统的基于统计概念和试验方法的可靠性保证技术，受到时间、经费和技术能力的限制，已经不能有效适应飞机产品的快速研制、高可靠性和长寿命设计的需求。同时，由于缝翼机构形式复杂，影响因素众多且各因素之间存在耦合作用，导致难以建立显式的运动学或动力学模型。所以以往的研究主要侧重系统级的失效，而对于其运动过程可靠性研究较少。

    随着计算机仿真技术的发展，利用商业软件对机构进行虚拟仿真与分析逐步受到越来越多学者的关注和广泛应用，仿真技术的应用有效的改善了实物试验方法的弊端。对于运动机构仿真，多采用多个软件平台。本文首先在CATIA中进行三维实体建模，在完成实体模型的基础上利用动力学分析软件LMS Virtual.Lab建立缝翼机构的动力学模型。与此同时在有限元软件Patran中建立缝翼机构关键部件的有限元模型；然后利用LMS Virtual.Lab与Patran的接口将多刚体模型中的关键部件用有限元模型替代并进行模态分析；最后将相关设计变量参数化形成最终缝翼机构的虚拟样机。

    在对前缘缝翼机构充分评估的基础上，基于多个软件平台，对缝翼机构进行了刚柔耦合仿真建模和动态性能分析，为缝翼机构的动态性能评估提供参考。最后，以机构运动卡滞为典型失效模式，以齿轮转速和齿轮齿条分度圆半径为随机变量，采用蒙特卡罗法进行了运动卡滞可靠性及设计变量归一化的可靠性灵敏度分析，得到的结果可以为缝翼机构的进一步优化设计提供有用信息。

1、前缘缝翼问题描述

    由于各段缝翼的结构形式相同，故研究中只取内段缝翼作为研究对象。飞机的前缘内段缝翼机构主要由缝翼翼面、三个支架、三个滑轨、两组齿轮齿条和安装在支架上的十二个滚轮组成。其中，支架与机身固接，在仿真中可看作静止部件，齿轮可以绕支架上的固定轴旋转，滑轨与翼面通过接头固接，齿条与滑轨利用螺栓固接，滚轮安装在支架上，可定轴转动。在缝翼工作时，位于缝翼两侧的操纵作动器同时驱动两个齿轮旋转，带动齿条运动，从而实现缝翼的收放。滑轨的轨迹受滚轮约束，在垂直转轴的平面内运动轨迹为圆弧，且三个滑轨的轨迹在同一个锥面上。前缘缝翼在20秒内的最大下偏角为20.85度（垂直转轴）。

    该缝翼机构是单自由度冗余驱动机构，翼面及滑轨只能绕与机翼固连的支架上的固定轴旋转，而由两个作动器同时驱动。在工作过程中如果两侧驱动速度不一致、齿轮齿条磨损、加工或安装误差过大都有可能导致机构运动不畅，阻力矩增加，严重时甚至出现机构卡死，对飞机性能造成严重影响。根据实际使用经验和FMEA分析，将其主要失效模式确定为机构卡滞，卡滞原因为内外侧运动不协调导致系统提供的驱动力矩不能克服各种阻力矩，缝翼无法正常收放而功能失效。引起该失效模式的典型因素选为齿轮的驱动速度和齿轮、齿条的分度圆半径。

2、分析模型建立

    2.1 多刚体模型

    建立了各部件的CATIA模型之后，导入动力学分析软件LMS Virtual.Lab中按照实际约束关系进行装配，并设置齿轮副参数、施加气动力和设置驱动。其中齿轮齿条参数取设计值；缝翼在收放过程中，气动力大小随着工作时间发生变化，在建模时，将气动力简化为垂直于翼面向上的若干个分布集中力，其大小用时间的函数表示；由于刚体模型中不能施加冗余驱动，故为了避免过约束现象，只对内侧齿轮施加速度驱动，使齿轮在规定时间内完成启动、运行、制动三个阶段。

    2.2 有限元模型建立

    有限元模型的计算精度和效率主要受到网格规模、网格质量。

    网格规模对计算效率的影响很大，建模时选择合理的柔性化部件和网格尺寸至关重要，在缝翼结构部件中，翼面和三个滑轨的刚度相对较弱，在工作过程中变形相对较大，故需要考虑其变形对机构动态响应的影响，建模时将其柔性化。由于翼面模型几何尺寸较大且内部结构和属性复杂，若采用实体网格则不但网格划分困难而且计算速度非常缓慢，故利用降维方法对几何模型进行合理简化。缝翼结构部件模型主要为板杆结构。其中蒙皮、隔板腹板简化为膜元；梁缘条、梁支柱、普通隔板缘条、上下蒙皮对接角材、简化为杆元；梁腹板、加强肋腹板、滑轨腹板简化为板单元；加强肋缘条简化为梁元。

    网格质量的好坏直接影响模型的计算精度。该网格用于动力学计算，主要关注模型质量阵和刚阵的合理性，为此所有网格的大小应趋于均匀，同时如果不关注高频影响，网格尺寸可适当选的稀疏一些。整个有限元模型包括个866个结点，1834个单元。

    2.3 刚柔耦合模型

    为了反映机构在运动过程中所产生的结构变形以及构件变形与整体运动之间的耦合作用等。必须建立其刚柔耦合仿真分析模型。而刚柔耦合模型的计算精度主要受模型的边界条件和柔性体模态的影响。

    用上述建立的有限元模型替代多刚体模型中的对应部件并进行模态计算和过滤，剔除频率过高的模态。

    刚柔耦合模型中系统的自由度增加，为了与实际一致，对外侧齿轮施加驱动。设内侧齿轮齿条分度圆半径分别为R₁、R₂，角速度分别为ω₁、ω₂；外侧齿轮齿条分度圆半径分别为R₁’、R₂’，角速度分别为ω₁’、ω₂’。则由缝翼的工作原理知内外侧齿条的转动角速度应相等，即ω₂=ω₂’。又由于内外侧齿轮和齿条的线速度分别相等，即

    所以，联立（1）与（2）得到：

    即内外侧齿轮转速应同步。

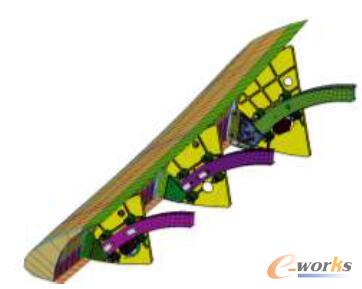
图1 缝翼机构刚柔耦合模型

    为了研究运动不协调对缝翼动态性能的影响，将内外侧驱动速度和各齿轮齿条的几何尺寸参数化，形成最终的刚柔耦合仿真模型，如图1所示。

3、仿真结果及影响因素分析

    3.1 缝翼刚柔耦合分析结果

    设置仿真时间为20秒，采用向后差分法进行求解，得到结果如图2-5所示：

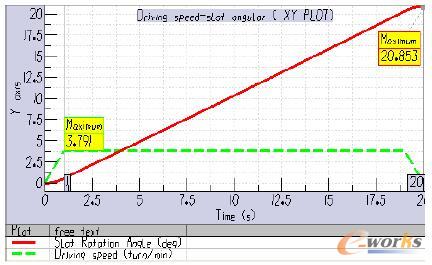
图2 驱动速度与缝翼转角曲线

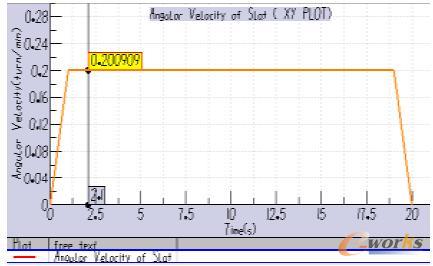
图3 缝翼翼面偏转角速度曲线

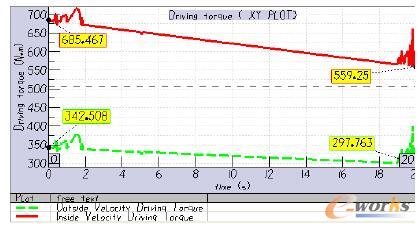
图4 内外侧齿轮驱动力矩曲线

    分析结果表明，当给定齿轮转速为先加速、再匀速、后减速时，缝翼在整个放下过程中，翼面的稳定转动角速度为0.201turn/min，最大偏角为20.85度。内侧齿轮上的驱动力矩最大为718N·m，最小驱动力矩为559.25N·m，外侧齿轮上的驱动力矩最大为400N·m，最小驱动力矩为298N·m，放下过程中内侧齿轮所需的驱动力矩要比外侧驱动力矩大，但两侧变化趋势大致相同，都是随着转动角度的增加有所减小，且在加速和减速阶段，驱动翼面所需的驱动力存在一定程度的波动。

    3.2 影响因素分析

    缝翼机构为齿轮齿条传动，依靠轮齿齿廓直接接触来传递运动和力，具有传递功率范围大、传递效率高等优点，但也存在对制造和安装精度要求高的缺点，加工、安装误差或磨损等原因会导致传动参数偏离设计值。另外两端齿轮的驱动速度在实际过程中也会存在偏差。这些都将引起缝翼运动的不协调。现选取外侧齿轮转速和外侧齿轮分度圆半径两个因素，研究其对缝翼收放动作的影响。

    （1）计算外侧齿轮转速变化时，内外侧驱动力矩的变化情况，结果如图5所示：

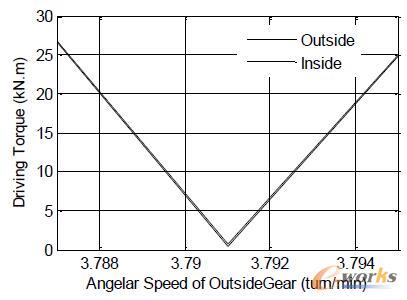
图5 外侧齿轮转速对内外侧驱动力矩影响

    可以看出，驱动缝翼转动时，需要内外侧作动器提供的力矩基本一致。随着齿轮转速偏离设计值，所需的驱动力矩急剧增加，这是由于转速偏离设计值之后，随着时间推移，齿轮的线位移不协调导致内外侧齿条的角速度不协调，因而缝翼旋转受阻，需要额外的输入功使结构产生一定的变形，从而导致所需的驱动力矩增加。且在设计值两侧是分段线性的。如果系统能提供的最大力矩已知，则可直接确定转速大致的允许范围。

    （2）计算外侧齿轮分度圆半径变化时，内外侧驱动力矩的变化情况，结果如图6所示：

    由以上仿真及拟合结果可以看出，随着齿轮分度圆半径偏离设计值，所需的驱动力矩急剧增加，这是由于转速偏离设计值之后，随着时间推移，齿轮的线位移不协调导致内外侧齿条的角速度不协调，从而导致所需的驱动力矩增加。且在设计值两侧是分段线性的。如果系统能提供的最大力矩已知，则可得到分度圆半径的大致允许范围。

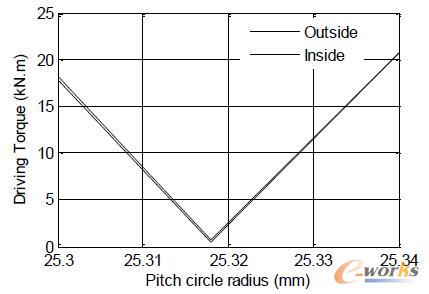
图6 外侧齿轮分度圆半径对驱动力矩影响

4、可靠性及灵敏度分析

    缝翼机构的刚柔耦合模型中，滑轨依靠与四个滚轮的接触力实现位置约束，且滑轨为柔性体，导致模型高度非线性，传统的近似解析法和函数替代法无法保证可靠性分析的精度。而Monte Carlo方法不受此类条件限制，且样本量较大的情况下计算精度较高，故采用Monte Carlo数字模拟法对缝翼进行可靠性分析。

    由实际使用经验及FMEA分析得知：缝翼卡滞为主要失效模式，卡滞的根本原因在于内外侧运动不协调时齿轮的最大驱动力矩[S]不能克服满足运动规律时所受的气动载荷及各部件的耦合阻力矩而导致的。以S(t)表示运动时域（0，20s）内缝翼所需的驱动力。则卡滞可靠性的功能函数可记为：

    [S]由翼面的操纵系统提供，可近似看作常数，而S（t）在缝翼转动过程中为变量。整个过程不发生卡滞的条件为g(t)>0(0≤t≤20s)。因此求解卡滞可靠度也即求解g(t)>0的概率。但S(t)为一过程量，随时间变化，统计特征复杂，为了求解方便，取S(t)在时域内的最大值S_max，则只要S_max<[S]就能保证缝翼不发生卡滞现象。

    由蒙特卡罗法基本原理知：失效概率的精确表达式为基本变量的联合概率密度函数在失效域中的积分，它可以改写为式（5）所示的失效域指示函数IF(x)的数学期望形式：

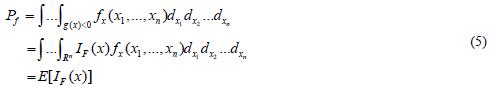
    式中，IF(x)为失效域的指示函数；R_n为n维变量空间；E[·]为数学期望算子。依大数定律，失效域指示函数的期望可以由失效域指示函数的样本均值近似。以随机变量的联合密度函数抽取N个样本落入失效域F内样本点的个数N_f与总样本个数N之比即为失效概率的估计值P_f，即

    为了比较不同分布参数对失效概率的影响，需消除基本变量量纲对可靠性灵敏度的影响，进行失效概率对分布参数的无量纲灵敏度分析，即

    对于正态变量

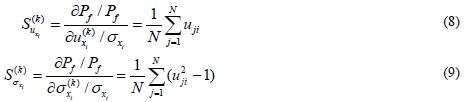
    式（9）中，u_ji为第j个样本xj=(x_j1,x_j2,…x_jn)的第i个分量x_ji所对应的标准正态样本，即u_ji=(x_ji-u_xi)/σ_xi。通过下式转换，可以得到与原始定义对应的可靠性灵敏度：

    选取气动力系数、齿轮齿条分度圆半径、和两端的驱动速度作为随机变量，其分布类型及参数如表1所示：

表1 随机变量选取及分布参数

    按照上述参数利用Matlab抽取10000组随机样本后代入仿真模型进行自动求解并将每组样本整个时间过程中缝翼所需的驱动力矩存入数据库中。计算结束后，查找每组样本整个过程中驱动力矩的最大值，即Smax(i)，其中(i=1,2,…,10000)。缝翼在整个工作周期内内外侧所需驱动力矩最大值的柱状分布图分别如图7（a）、（b）所示，其中内侧所需驱动力矩的最大值为51.26kN·m，最小值为0.571789kN·m；外侧所需驱动力矩的最大值为51.17kN·m，最小值为0.29326kN·m。

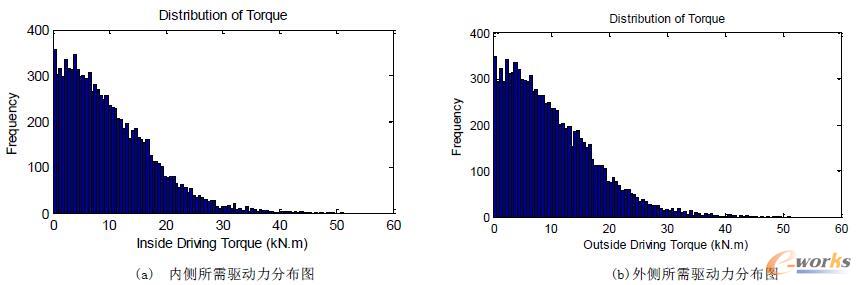
图7 内外侧驱动力矩分布柱状图

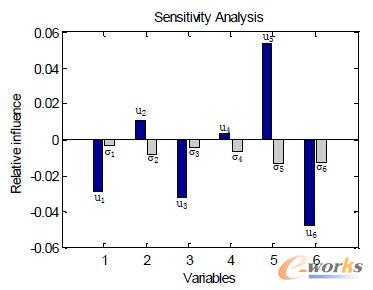
图8 随机变量灵敏度分析

    缝翼机构由两端的两个作动器同时驱动，可看作串联系统，即当任何一端卡滞时认为系统失效。该缝翼机构的旋转作动器所能提供的最大驱动力矩为40kN·m，则由（6）式求得系统的可靠度为0.9967。

    编程计算无量纲的可靠性灵敏度，得到消除量纲影响后各变量分布参数对失效概率的相对影响结果如图8所示，其中蓝色代表变量均值对可靠度的影响，灰色代表变量方差对可靠度的影响。

    从灵敏度分析结果看出，齿轮转速对缝翼机构的可靠度影响最大，当两端转速不协调时系统可靠度下降，故实际中需要监控两端转速，并进行实时调节。齿轮分度圆半径对可靠度也有较大的影响，应该严格控制其加工及安装精度；而齿条的分度圆半径对失效概率的影响较小，可适当放松要求。

5 结论

    （1）以典型飞机前缘缝翼运动机构为对象，利用多个软件平台，建立了参数化的刚柔耦合仿真模型。在此基础上对缝翼机构进行了动态性能分析，得到了相关动态响应量。

    （2）选取齿轮转速和齿轮分度圆半径为影响因素，分析了其参数变化对缝翼运动的影响规律。

    （3）在充分评估的基础上，以内外两侧运动不协调卡滞为典型失效模式，采用蒙特卡罗法进行了前缘缝翼机构运动卡滞可靠性及各设计变量对可靠度的灵敏度分析，其结果为缝翼的进一步优化设计提供了参考数据。