圆筒类零件一般采用冲压连续模具进行生产,此类模具对工艺的要求较高,如果工艺设计不合理,模具会频繁修模甚至会报废,所以需要对工艺设计进行仿真验证,以减少后期设变风险,多工步拉深工艺的验证可以使用LS-DYNA进行仿真分析,现在业界通用的前处理软件,冲压分析一般使用壳单元,2号单元,默认采用显式算法,但是多工步分析过程,显式算法的动力效应导致的误差会逐步累积,所以需要对网格、单元类型、求解算法进行适当的调整,以保证结果的准确性。下面以一个筒形件为例,对分析过程进行详细说明:
产品3D
工艺设计
进行合理的多工步优化设计,如果尺寸设计不合理,拉深过程会异常减薄,导致产品不能正常生成,分析过程也会异常终止。
仿真分析验证
1.板材网格优化
在硬件允许的情况下,不开启网格细化,需要提前优化板材网格。
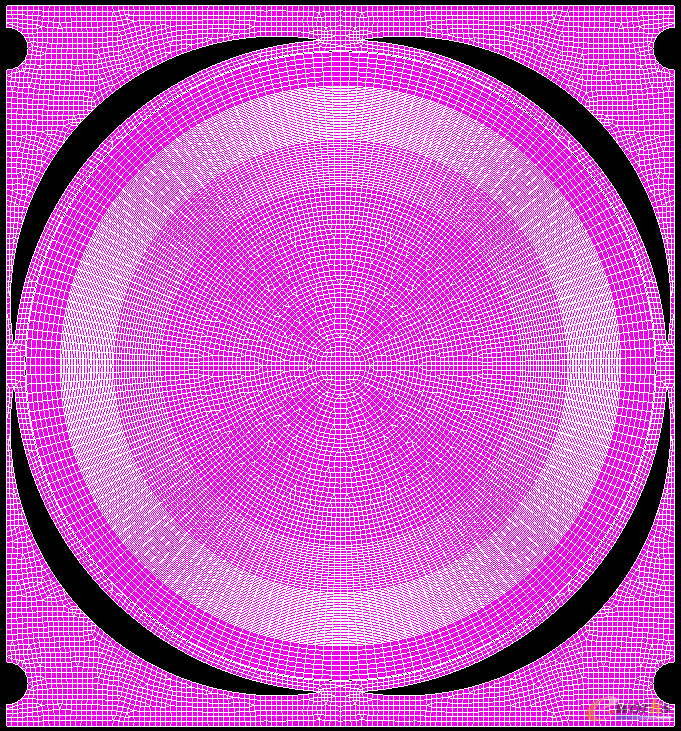 优化板材网格
优化板材网格
LS-DYNA中,可以应用于壳单元的材料主要是36号材料和37号材料,这两种最大的区别就是屈服准则的差异;36号材料基于Barlat 1989(3参数模型),37号材料基于Hill 1948(标准Hill各向异性模型)屈服准则。
36号结果
37号结果
反应到结果上,36号材料在不同方向的流动不一致,37号是各方向均匀的收缩流动。分析前需要对材料了解充分,对于各向异性差异不大的材料,可以采用37号材料,对于各项异性比较大的材料,建议采用36号材料。
3.分析算法的选择
一般采用LS-DYNA进行冲压分析,如果拉深工步较少,可以使用显式算法,但是当拉深步数增多后,分析结果误差会增大。
7工步显式算法结果
在前2步显式算法和隐式算法厚度结果差异不大,但是随着步数增多,厚度分布趋势差异较大,隐式算法的结果分布更合理,在多工步分析中,选择隐式分析,结果会更精确。
7工步隐式算法结果
4.单元类型选择
目前在lS-DYNA中,用于冲压壳单元计算主要是2号和16号单元,默认显式算法是2号,隐式算法是16号。
2号单元-Belytschko-Tsay壳单元
基于Belytschko-Tsay理论,采用缩减积分(Reduced Integration),计算效率高。每个单元仅需1个积分点(沿厚度方向可设置多个积分点)。计算速度快,适合大规模模型。对薄板和中厚板问题表现良好。可能存在剪切自锁(Shear Locking)问题,尤其在弯曲变形中。对翘曲(Warping)或复杂应力状态的处理能力有限。
16号单元-全积分Belytschko-Wong-Chiang壳单元
基于Belytschko-Wong-Chiang理论,采用全积分(Full Integration),每个单元使用2×2个积分点。更多积分点提高了计算精度,但代价是更高的计算成本。显著减少剪切自锁问题,适用于弯曲主导的工况。对翘曲和复杂应力分布的模拟更准确。计算时间比2号单元长(约2倍)。可能因过度刚度(Over-stiffness)导致局部响应偏差。适用场景需要高精度的静态或准静态分析(如钣金成形),复杂弯曲或剪切变形占主导的问题。
在算力允许的情况下,建议使用16号单元。
5.求解器的选择
LS-DYNA求解器分为SMP和MPP,从计算效率看,显式算法在网格数目不多的情况下,可以选择SMP版本,如果是隐式算法,建议选择MPP版本,从LS-DYNA的目前发展看,以后主要还是MPP或者HYB版本了,SMP版本会逐步退出历史舞台。
MPP-隐式算法结果
MPP-显式算法结果
SMP-显式算法结果
6.分析效率对比
从分析时间看,此类零件的分析过程,隐式计算过程顺利,没有不收敛的情况,计算效率反而会比显式算法更快;2号单元的效率比16号单元更高效,结果基本没有差异;显式计算,最新的R16.1求解器效率有明显提升。
小结
多工步筒形拉深件仿真分析,在使用LS-DYNA分析时,需要对网格、材料类型、单元类型、分析类型、求解器类型进行调整,才能得到相对比较理想的结果;对于此类件,单工步的变形相对没有太复杂,所以建议使用隐式算法+16号单元+MPP求解器进行分析。
本文为e-works原创投稿文章,未经e-works书面许可,任何人不得复制、转载、摘编等任何方式进行使用。如已是e-works授权合作伙伴,应在授权范围内使用。e-works内容合作伙伴申请热线:editor@e-works.net.cn tel:027-87592219/20/21。