0 引言

    膜片弹簧是碟形弹簧的一种，膜片弹簧的优化大致包含三个方面，首先是选型优化，即根据设计工程师提供的设计空间尺寸与载荷变形特性曲线要求，膜片弹簧生产厂家采用自编的程序，输入数据库中已有的接近设计尺寸的一组结构参数，经过计算输出载荷与变形特性曲线，将该曲线与设计工程师要求的曲线进行对比，两条曲线的差异大小决定了生产厂家是否对膜片弹簧的结构参数进行再次的优选，直至两条曲线比较接近或者符合厂家的要求为止，并输出优化后的结构参数;其次，对特性曲线进行优化，主要通过调整多组参数对膜片弹簧的总体性能曲线进行优化评估，使之适应离合器的需要。这种优化相对于选型优化，空间尺寸的限制要弱一些，将优化空间进一步放大，往往也加入优化算法，能够优化出设计厂家需要的更好的性能曲线，并再次对优化的结构参数进行圆整或修改使之符合生产厂家材料型号或生产工艺的需要。再者就是膜片弹簧的强度优化，主要是大致在满足膜片弹簧性能特性曲线的基础上，对结构上关键点位应力的进行优化，主要是局部参数的调整，如导角半径、制造工艺的改进以及主要结构参数的微小调整，以达到降低膜片弹簧关键点处结构应力的目的。

    2 膜片弹簧的载荷位移特性设计计算

    膜片弹簧特性曲线类似Belleville弹簧（蝶形弹簧)，因为膜片弹簧是具有分离指的改进的蝶形弹簧。为了设计膜片弹簧，其中最重要的是要获得理想的膜片弹簧载荷与变形特性关系曲线。这个特性曲线决定了膜片弹簧的基本尺寸及其结构特点。膜片弹簧设计计算主要依据A-L公式，也有其它计算公式，但是大部分是依据A-L公式并对其进行修正的。

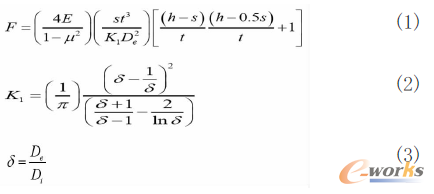
    上述公式（1)中：δ为膜片弹簧内外直径之比De/Di，泊松比μ=0.3,E=弹性模量，Di为膜片弹簧内径，s为膜片弹簧变形量，t为膜片弹簧厚度，De为膜片弹簧外径，h为膜片弹簧自由高度。通过上述A-L公式设计了某离合器C1膜片弹簧的结构参数及其特性曲线，分别见图1与图2。由于在初始设计时，均是通过公式（1)不断试算，通过调节膜片弹簧的结构参数，以便获得基本符合客户需要的载荷位移特性曲线。这种通过A-L公式的多次计算优选并没有使膜片弹簧的特性曲线得到真正的优化，即没有在真正的设计空间里穷尽所有方案而得到了最优解。

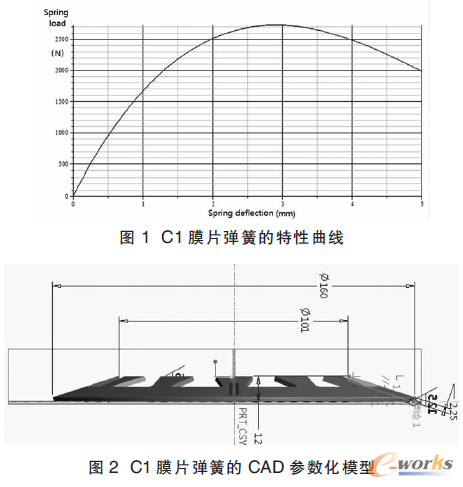
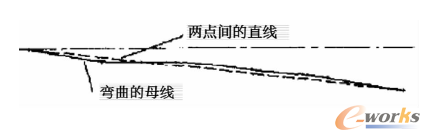
    其实，A-L公式也存在一定的局限性。A-L公式假设膜片弹簧在载荷的作用下，其碟形部分的子午端面只能绕中心锥面某一点转动，而矩形截面本身不变形，这种刚体假设与矩形截面发生了弯（屈）曲变形并不相符，由于弯曲变形导致了膜片弹簧力的作用点的改变、刚度的变化以及支承部位产生了径向力等。这种弯曲变形通过有限元软件的分析计算，根据结果绘制的碟形部分和分离指的母线，如上图中的斜的曲线所示，从图中可以看出受到载荷作用后的母线并非直线。