0 引言

    橡胶减振器因其阻尼性能好、结构简单、价格低廉等优点，在航天、船舶、汽车等工程领域得到广泛应用。但由于橡胶的复杂的非线性力学行为，缺乏准确的材料模型来描述其特性，使得橡胶减振器的选型和设计主要依靠工程经验和试验方法，耗费大量人力物力。随着有限元技术和计算机技术的发展，作为先进的非线性有限元软件一ABAQUS已经具备超弹性、粘弹性橡胶模型和体积不可压缩材料大变形的有限元计算功能，这为橡胶减振器的有限元分析提供了极大的便利。

1 橡胶减振器非线性有限元分析

1.1 橡胶减振器非线性特性

    橡胶减振器非线性主要来源于几何非线性、材料非线性、边界非线性。其中几何非线性指橡胶为体积不可压缩材料，其在工况中会出现大弹性形变，已不能用小形变理论分析；材料非线性指橡胶材料为粘弹性材料，其应力-应变曲线为非线性的，且动态特性与频率、振幅、温度相关；边界非线性指橡胶材料与金属的接触过程中，其边界条件在分析过程中发生变化。在ABAQUS中，几何非线性即大变形可在分析步(Step)中选择开启，开启后在分析过程中会考虑到几何非线性;材料库中有丰富的材料可供选择，对于橡胶材料可选择超弹性、粘弹性；ABAQUS中在相互作用（Interaction)内定义各部分之间的相互作用，对于边界非线性可定义橡胶与金属支架之间的接触，通过接触算法实现边界条件非线性和力的传递。

1.2 橡胶材料参数的确定

    在有限元方法中，常把橡胶近似视为不可压缩材料，使用超弹性本构模型描述其弹性能力，其中的Mooney-Rivlin本构模型如下

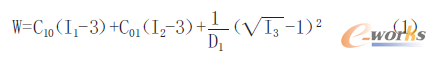
    其中，I1、I2、I3是应变不变量，C10、C01、D1是由材料决定的常数。当D1=0时，橡胶完全不可压缩。Mooney-Rivlin模型可以仅使用C10、C01和D1三个常数，较精确地刻画在橡胶元件工作于中小应变时的弹性能力。

    材料常数C10、C01和D1的确定，需要进行一系列的复杂试验。由超弹性材料常数C10/C01与橡胶的邵氏硬度HS有如图2的经验关系。而对于可自由变形的橡胶元件，其剪切模量G(MPa)与材料常数C10、C01有关系：

    则对于选定硬度的橡胶材料，通过图确定C10/C01的值，在代入式(2)中，可以求解出材料常Cl0、C01。

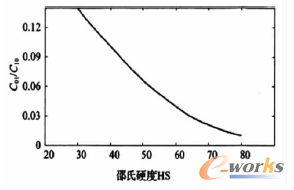
    图1 材料常数与邵氏硬度的经验关系

    本文所用橡胶减振器橡胶为某型号硅橡胶，其弹性剪切模量为2MPa，邵氏硬度为50。通过经验公式得到材料参数如表1。

    表1 橡胶超弹性模型本构模型参数取值

    除了要定义橡胶的超弹性材料参数外，还需要定义材料阻尼以及粘弹性参数。在ABAQUS中提供了多种阻尼模型:瑞利阻尼、结构阻尼、模态阻尼、全局阻尼。对橡胶选择材料阻尼(Damping)中的瑞利阻尼。

    由手册可确定该硅橡胶的损耗因子为0.2,根据损耗因子P与临界阻尼比β之间的关系：

    可得临界阻尼比为0.1。为了方便计算需将临界阻尼比转化为瑞利阻尼。瑞利阻尼可表示为

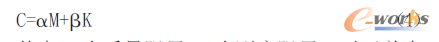
    其中α为质量阻尼，β为刚度阻尼。对于单自由度系统，临界阻尼比与瑞利阻尼的关系为:

    假设在低频段和高频段(5Hz?400Hz)，系统具有相差不大的临界阻尼比，则可确定瑞利阻尼值α为0.988,β=0.00049。

1.3 建立橡胶减振器模型

    为了研究其减振性能，将T型橡胶减振器与支架结构和质量块组合在一起，结构如图2。将减振器整体几何模型导入Hypermesh中划分网格，然后导入ABAQUS中进行参数设置和分析。

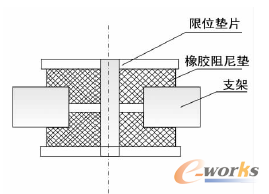
    图2 T型橡胶阻尼垫结构剖面图

    在有限元模型中，由于垫片与橡胶在实际运动中发生较小的位移，所以它们之间的相互作用定义为绑定约束(Tie)4。橡胶垫与支架在实际运动中既有相对的位移，也有力的传递，所以它们之间的相互作用定义为面面接触(SurfacetoSurface)。接触属性可定义接触面之间的法向行为和切向行为。法向行为是指接触面之间法向力的传递方式，这里选择’’硬接触’’即接触面之间传递的力的大小不受限制，当接触力变为零或者负值时，两个接触面分离，并且去掉相应节点上的接触约束。切向行为是指接触面之间切向的力学作用，常见的方式是定义库伦摩擦，通过摩擦系数来表示接触面之间的摩擦特性。如图3所示是单自由度橡胶减振器系统的有限元模型。