0 引言
由于飞机地面运动品质和操纵特性的研究直接关系到飞机起降的安全,评估飞机地面操纵运动时的响应对于飞机的设计和飞行安全有重要意义,故现代飞机对飞机地面运行特性的要求越来越高。而现有对飞机地面特性的研究主要集中在飞机的着陆缓冲、滑行减震、前轮转弯、刹车操纵等方面,但对于飞机的非对称操纵动力学(侧风滑跑或一侧主轮胎泄气)方面的研究却少之又少。而在实际情况中,飞机在地面滑行期间由于风速的影响,经常受不对称载荷的作用,故对这一方向的研究的重要性不言而喻。
飞机在受非对称载荷作用下,可对机体进行全面的受力分析,从而建立飞机最后在平衡状态下直线滑跑的数学模型。但是更为关心的是飞机在受非对称载荷影响到最后保持直线滑跑的过程中,飞行员操纵飞机前轮尽可能使飞机不偏离初始轨道这一调节过程,因为绝大部分事故将发生在此阶段,而这一调节过程却很难建立一个准确的数学模型来描述,基于此本文建立了一套有效的闭环控制系统模型,来模拟飞机滑跑时受不对称载荷作用下的动态响应过程。
本文主要从飞机滑跑过程中所受侧风影响为出发点,首先建立了飞机受恒定侧风影响,最后静力平衡状态下的数学模型,并对此状态进行数值求解。随后在郭孔辉院士的预瞄跟随理论基础上,提出一套适用于飞机的侧向偏移控制算法,并结合PID控制策略在Amesim中建立了飞行员方向控制模型并进行飞机侧风稳定性虚拟试验。本试验中采用多体动力学软件LVM建立了完善的飞机模型,高自由度的飞机模型能充分反映出实际飞机复杂的非线性特性,以此检验闭环系统的控制效果更加接近实际情况。
1 飞机侧风滑跑操纵动力学模型
1.1 数学模型的建立
飞机地面滑行期间,由于侧风引起的不对称载荷,与地面作用于飞机轮胎上的侧向载荷抗衡(见图1)。该侧向载荷引起前、主轮胎不一致的偏航角,为了保持飞机直线滑行需偏转前轮,使前、主轮有相同的速度方向。
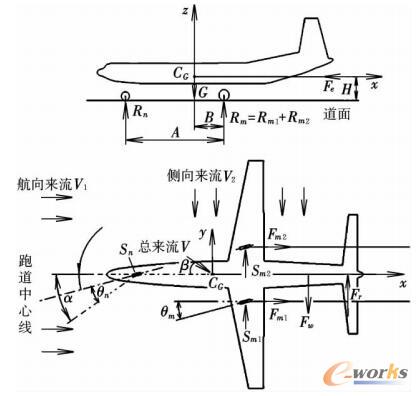
图1 侧风影响下操纵飞机地面运动静力平衡
前、主轮胎运动方向一致,且偏航角函数关系为:
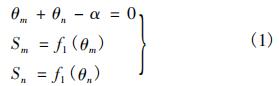
其中:
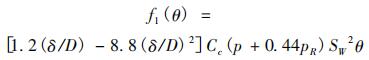
方向舵偏角与前轮操纵角关系为:
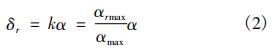
方向舵侧向力关系为:
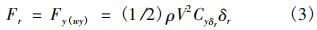
根据飞机受力关系图可以建立该平衡状态的运动方程组:
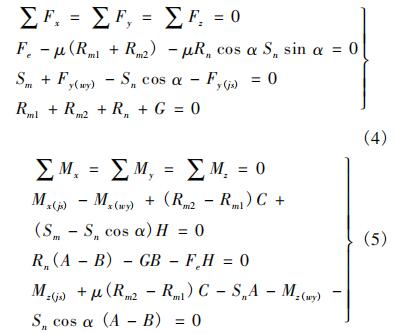
以上各式中,Fe为发动机推力;μ为轮胎与地面的滑动摩擦系数;Rm1为左侧主轮载荷;Rm2为右侧主轮载荷;Rn为前轮载荷;α为前轮转角;Sn为前轮侧向力;Sm为主轮侧向力;θm为主轮偏航角;θn为前轮偏航角;Fw为机体所受侧风影响下的侧向力,可向飞机质心方向等效为一个力与两个力矩Fjs,Mx(js),Mz(js);Fr为飞机偏转舵面所产生的侧向力,可向飞机质心方向等效为一个力与两个力矩Fwy,Mx(wy),Mz(wy);G为飞机所受重力;SW为机翼面积;A为前、主轮距;B为主轮与飞机质心的间距;C为半主轮距;H为地面与飞机质心的间距。δ为轮胎压缩量;D为轮胎外直径;Cc为轮胎偏航系数;p和pR分别为轮胎实际充气压力和轮胎额定充气压力;ρ为空气密度;V为空气来流速度。
1.2 气动力的计算
模型中气动力的计算中,因为由侧风产生的侧滑角对飞机的影响占主要因素,故忽略飞机迎角的影响。由于侧向来流的作用,使总来流方向与飞机对称面成一夹角β,此时作用于飞机上的气动力是左右不对称的,由此将会出现侧向力Fjs、滚转力矩Mx(js)和偏航力矩Mz(wy)。方向舵的偏转角度δ亦会对飞机产生侧向力Fwy、滚转力矩Mx(wy)和偏航力矩Mz(wy)。在机体轴系中可用下式表示:
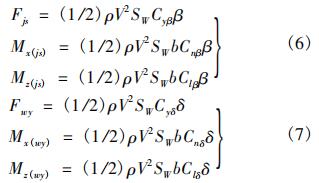
式中,b为机翼展长;β为侧滑角;δ为方向舵偏角;Cyβ,Cnβ和Clβ分别为侧力系数、偏航力矩和滚转力矩对侧滑角的导数;Cyδ,Cnδ和Clδ分别为侧力系数、偏航力矩和滚转力矩对方向舵偏角的导数。
1.3 数学模型的求解
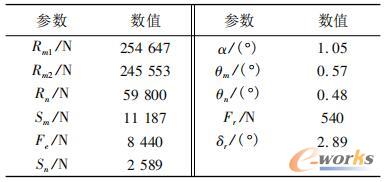
给定飞机的航向速度V1=20m/s,侧向风速V2=6m/s,通过求解上述的非线性方程组,对未知参数的求解结果如表1所示。
表1 平衡状态下的方程数值解
2 飞机侧风闭环控制系统模型的建立
整个飞机侧风闭环控制系统模型如图2所示。给定飞机一个驱动速度v,其中侧风作为外部扰动作用于飞机模型,使得飞机的实际行驶轨迹与预期轨迹间产生一个侧向偏移y,飞机运动状态由传感器感知并实时反馈给飞行员模型。飞行员通过控制算法求解出前轮转角α后作用于飞机模型。
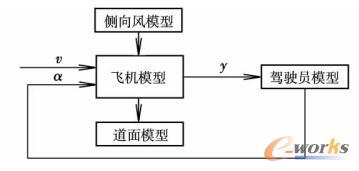
图2 飞机—侧风闭环控制系统
2.1 建立飞行员模型
根据预瞄控制理论的思想,考虑飞机在预定的道面上滑跑。其轨道中心线方程为f(t),在某一瞬时t时刻,飞机的瞬时状态为y=y(t),ý=ý(t)。此时飞行员向前预视一个前向距离d,对应的“预瞄时间”为T=d/v,其中v为飞机的滑跑速度,飞行员前视点的横向坐标为f(t+T),此时飞行员将控制前轮偏转一定的角度,对应飞机的轨迹曲率为1/ρr,横向加速度为ÿ(t),这样在经过时间T以后,在t+T时刻飞机的横向位移为:
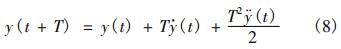
根据“最小误差原则”,飞行员总是希望选择一个最优的轨迹曲率1/ρr,使得飞机在滑行距离d(经时间T)后,其横向位置y(t+T)与该处的预期轨迹座标f(t+T)相一致。将ÿ(t)=v2/ρr,d=vt代入式(8)得到最优曲率为:
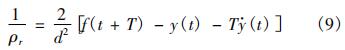
飞机沿地面作高度不变的平面运动,如图3所示。
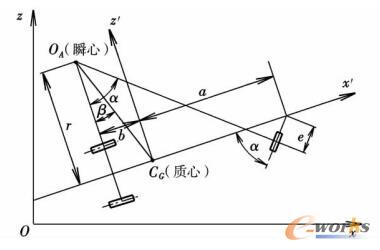
图3 飞机地面运动受力图
由图可知,与飞机有关的几何关系有:
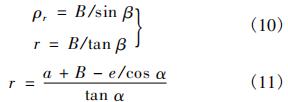
得:
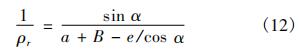
式中,ρr为飞机偏转前轮时对应的曲率半径,即为图中飞机质心O与瞬心OA之间的距离;a为前轮与飞机质心的距离;e为前轮稳定距;r为OA与两主轮中心点的间距。
考虑飞机在中速滑跑时,靠舵板机实现偏转前轮转角α,前轮相对于中立位置向左右偏转的极限位置仅在8°左右,此时sinα≈α,cosα≈1,故上式可简化为:
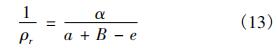
代入式(9)得到理想的飞机前轮偏角为:
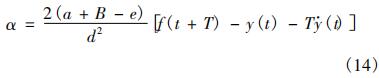
考虑到飞机动力学系统很强的非线性特性,故无法用一个简单的传递函数来表示飞机前轮转角与飞机横向轨迹之间的传递关系,故本文在以上预瞄控制理论的基础上又引入了PID控制来调节前轮转角的输入。
2.2 建立飞机地面运动虚拟样机
LMS公司专门为模拟机械系统真实运动和载荷开发的LVM软件,采用笛卡尔坐标法进行多体系统动力学建模,生成的微分代数方程组为:
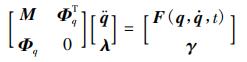
式中,q,q′,q″分别为系统的位置、速度和加速度向量;λ∈Rn为拉格朗日乘子;t∈R为时间;M∈Rm×n为质量矩阵;Φq∈Rm×n为约束雅克比矩阵;F(q,q′,t)为作用力;γ为加速度公式中二阶导数项。
研究者只需给出各个部件间的约束关系和质量、转动惯量等属性,并建立轮胎和空气动力等基本力学元素,软件就会自动生成微分代数方程组,并利用内嵌的处理数学模型计算方法和数值积分方法自动进行程序化处理,得到运动学规律和动力学响应。虚拟样机如图4所示。
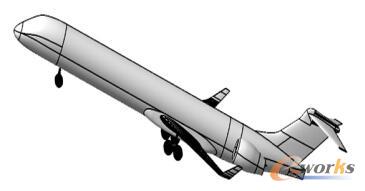
图4 全机地面运动虚拟样机
2.3 实现联合仿真
根据公式并采用PID控制策略在Amesim中建立了飞行员方向控制模型,与LVM中飞机模型的结合是通过定义节点变量实现的。在LVM中定义了飞机模型的输入节点变量α为前轮转角,以获取由飞行员模型计算得到的前轮转动角度,输出节点变量为横向偏移y和飞机横向速度v,以作为飞行员模型的反馈输入。本文联合建模的飞机侧风稳定性闭环系统如图5所示。

图5 飞机侧风闭环控制系统模型
3 联合仿真与结果分析
飞机侧风稳定性试验工况为直线行驶,给定飞机滑跑速度为20m/s,受恒定6m/s侧风影响。侧风影响下飞机质心处所受的气动载荷,由于方向舵偏角受前轮偏转的影响,Fy,Mx,Mz在前轮未保持平衡状态时,会发生一定变化,如图6~图8所示。
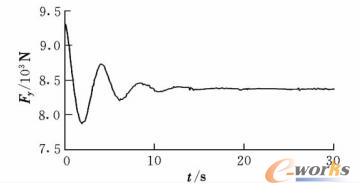
图6 侧风下飞机所受侧向力
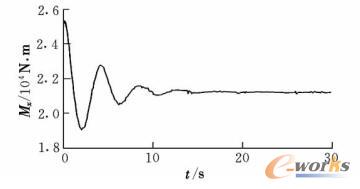
图7 侧风下飞机所受横向力矩
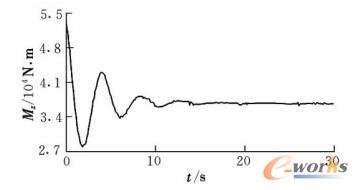
图8 侧风下飞机所受航向力矩
图9为未加控制系统时飞机质心处的横向轨迹,图10为有控制系统时飞机质心处的横向轨迹,图11为前轮转角的变化曲线。结合图9和图10可以看出,未加控制系统时,飞机在受侧风影响下会逐渐偏离跑道中心线,而且随时间变化越来越大,很容易发生危险,而加入控制系统后飞机的侧向偏移得到了很好的控制,最大横向偏移量仅为0.9m左右,而且随时间变化飞机将逐渐回归到原跑道中心线,避免了危险的发生。结合图10和图11可以看出,飞机前轮转角最终趋于一个恒定值,而飞机的横向轨迹曲线也逐渐向跑道中心线靠近,并最终与中心线重合,此时的状态即为飞机受恒定侧风影响,飞行员进行前轮偏转而最终保持的静力平衡状态,此时飞机将沿着跑道中心线保持直线滑行。
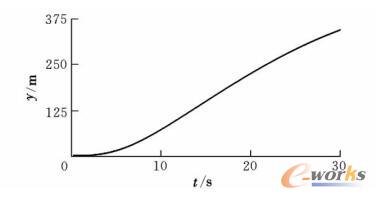
图9 飞机质心处的横向偏移(无控制)
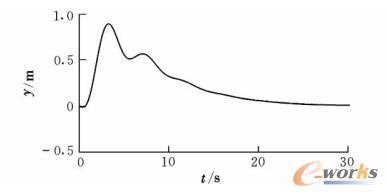
图10 飞机质心处的横向偏移(有控制)
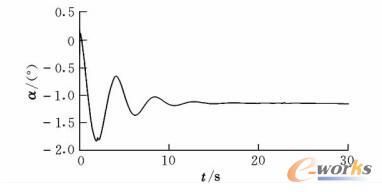
图11 飞机前轮操纵角度
图12~图16为飞机各机轮的载荷变化曲线,最终随着时间也趋于恒定的值,稳态下的值即对应飞机受侧风影响下的静力平衡状态。
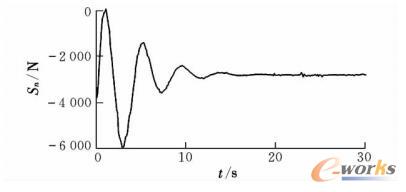
图12 飞机前轮所受地面侧向力
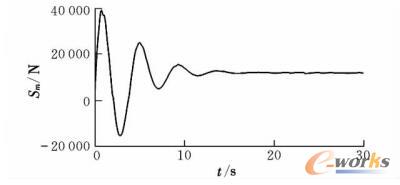
图13 飞机主轮所受地面侧向力
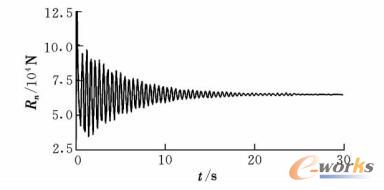
图14 前起机轮垂直载荷
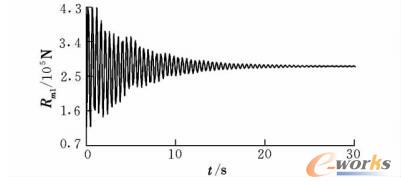
图15 左侧主起机轮垂直载荷
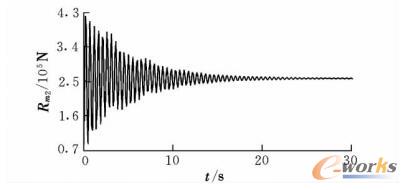
图16 右侧主起机轮垂直载荷
将飞机最终沿跑道中心线稳定滑跑状态下的主要参数进行记录,并与表1中计算得出的平衡状态下的数值解进行对比,结果如表2所示。
表2 方程解与仿真解对比
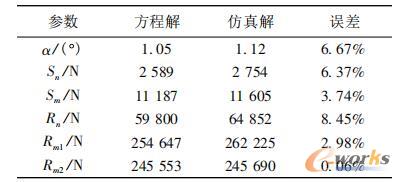
对比上表中的方程数值解与仿真稳态解可以看出,两者结果相差较小,两者的相对误差都在10%以内,说明利用此闭环控制系统来进行飞机滑跑时的侧风纠偏,最终得到的飞机稳态响应是正确的,从而验证了用此闭环控制系统来模拟飞机受不对称载荷作用下的动态响应过程的可行性。
4 结束语
本文基于预瞄跟随理论,结合PID控制策略,利用Amesim建立了一套飞行员驾驶模型,采用Lms.Virtual.Lab Motion建立了某民用飞机的动力学模型,通过两者联合仿真来进行其侧风稳定性分析,结果表明此飞行员模型能有效控制飞机的侧向位移,为今后研究飞机在不对称载荷影响下的地面操稳特性、以及飞机智能操纵系统方面奠定了基础。
本文来源于互联网,e-works本着传播知识、有益学习和研究的目的进行的转载,为网友免费提供,并以尽力标明作者与出处,如有著作权人或出版方提出异议,本站将立即删除。如果您对文章转载有任何疑问请告之我们,以便我们及时纠正。联系方式:editor@e-works.net.cn tel:027-87592219/20/21。