1 概述

    汽车动力总成悬置系统由动力总成和悬置系统组成，动力总成包含动力源和变速箱两部分。动力总成通过悬置系统与汽车车架连接，悬置系统的作用：（1）支撑动力总成的重量；（2）隔离从动力总成传递到车身上的振动；（3）吸收路面经由悬架传递到车身上的振动；（4）限制动力总成系统在大扭矩及极限行驶工况下的位移。

    纯电动汽车动力总成悬置系统与传统内燃机汽车动力总成在结构上最大的区别就在于其动力源来自驱动电机，而不是内燃机。驱动电机在加速时电机会产生转矩波动，引起动力总成振动，电机转子由于不平衡质量而引起的振动也会直接作用在动力总成上，这些振动会传给车架，易导致整车纵向和垂向振动。悬置系统作为汽车振动系统的一个重要子系统，在悬置系统某一个自由度方向作用变化的激振力，并引起该方向的振动时，导致其他自由度方向的振动，出现耦合振动。由于耦合振动扩大了振动频率的范围，为了达到相同程度的减振效果，悬置需要进行解耦，悬置解耦主要取决于悬置系统的结构形式、布置方式和刚度等。为了解决动力总成悬置系统振动耦合问题，采用多目标优化方法对悬置系统进行优化来降低振动耦合，提高悬置系统的隔振性能。

    本文以某款电动汽车动力总成为研究对象，动力总成简化为刚体建立多体动力学模型，以悬置安装位置和刚度为设计变量，固有频率为约束条件，模态解耦率为优化目标，利用MotionView/MotionSolve/HyperStudy对悬置系统进行设计优化。优化结果表明，通过优化悬置安装位置和刚度使得固有频率分布合理，有效的提高了模态解耦率。

2 动力总成悬置系统模态解耦分析

    2.1 模态解耦基本理论

    模态解耦是指作用在系统某个方向的力所做的功全部转化该方向的能量，即某方向的激振力只能引起该方向上的振动。系统的解耦程度用模态解耦率来表示，模态解耦率是指在某一阶模态下的能量占总能量的百分比。当模态能量占总能量的98%时，表明在该频率下该模态起主导作用，其解耦程度非常高；当每阶模态的解耦率均为100%，表明它们彼此独立，可以将每阶模态当作单自由度系统。模态解耦率的计算方法：

    1）计算动力悬置系统的固有频率和主振型

    将动力总成悬置系统简化为自由振动系统，因为阻尼对系统的固有特性影响较小，故该系统的振动微分方程为

    式中：M为系统的质量矩阵；X为系统的位移；K为系统的刚度矩阵。

    式（1）的特征方程为

    式中：ω_i为圆频率，ω_i=2πf_i，其中f_i为第i阶固有频率。

    通过式（2）计算得到动力总成悬置系统的固有频率为f1，……，f6（对应的圆频率分别为ω1，……，ω6）。

    该系统的齐次线性方程为

    式中：A_i为固有频率fi对应的振型向量。

    2）计算某个模态的动能

    3）计算模态解耦率

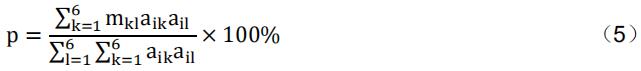
    2.2 建立动力总成悬置系统六自由度刚体模型

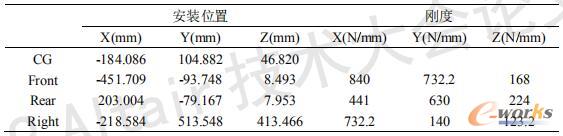
    本文以某电动汽车动力总成悬置系统为优化对象，驱动电机和减速器简化为刚体，悬置系统简化为空间三向正交弹簧元件，利用MotionView建立动力总成悬置系统六自由度刚体模型如图1所示。动力总成悬置系统质量为75.8Kg，质心和悬置安装位置见表1，悬置刚度见表2。

图1 动力总成悬置系统多体模型

表1 质心和悬置安装位置及刚度

    2.3 模态解耦率分析

    动力总成悬置系统在空间可以沿x、y、z轴三个方向平动和绕x、y、z轴三个方向转动，共六个自由度，因此存在6阶固有频率。利用MotionSolve求得动力总成悬置系统固有频率及模态解耦率的结果如表2。

表2 动力总成悬置系统固有频率及模态解耦率

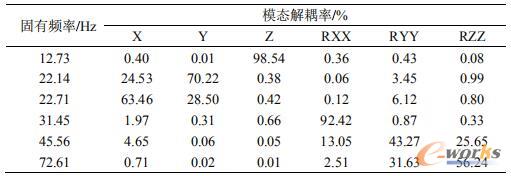
    从表2可以看出：第一阶固有频率为12.73Hz，沿Z轴方向平动，模态解耦率为98.54%；第二阶固有频率为22.14Hz，沿Y轴方向平动，模态解耦率为70.22%；第三阶固有频率为22.71Hz，沿X轴方向平动，模态解耦率为63.46%；第四阶固有频率为31.45Hz，绕X轴方向转动，模态解耦率为92.42%；第五阶固有频率为45.56Hz，绕Y轴方向转动，模态解耦率为43.27%；第六阶固有频率为72.61Hz，绕Z轴方向转动，模态解耦率为56.24%。第二阶与第三阶频率间隔为0.57小于1。第二、三、五、六阶模态解耦率小于90%，解耦程度较低。因此，需要对动力总成悬置系统进行优化，增大固有频率间隔，提高模态解耦率。

3 动力总成悬置系统解耦优化设计

    3.1 设计变量

    动力总成悬置系统的耦合程度与悬置系统的刚度、安装位置和安装角度等因素有关。考虑到整车布置空间，选取悬置安装位置和刚度为设计变量，每个悬置三个方向的位置和三个方向的刚度，共计18个设计变量。

    3.2 约束条件

    由机械振动理论得知，当系统模态频率低于激励频率的0.707倍时，系统才能有效的隔离振动。电动汽车常用车速为30km/h～80km/h，可计算出系统的最大频率为55Hz。考虑到来自路面的激励，系统频率需大于5Hz。为了避免频率太近，引起两个方向同时振动而造成振动耦合，固有频率的间隔都要大于1Hz。

    3.3 优化目标

    选取电机动力总成悬置系统的6阶模态对应的能量解耦率作为优化目标，每阶模态解耦率均要大于90%，保证每阶解耦程度较高。

    3.4 优化算法

    HyperStudy具有DOE灵敏度分析、拟合分析、设计优化等功能。为用户提供了多种实用、有效的优化算法。针对多目标优化问题，提供了全局响应面法、多目标混合算法和多目标遗传算法等算法.本文采用了多目标遗传算法进行求解优化，动力总成悬置系统优化后的悬置安装位置和刚度见表3，优化后的固有频率及模态解耦率见表4。

表3 动力总成悬置系统优化后的悬置安装位置和刚度

表4 动力总成悬置系统优化后的固有频率及模态解耦率

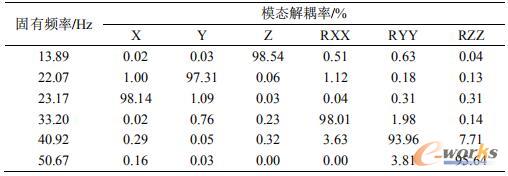
    从表4可以看出：第一阶固有频率为13.89，第六阶固有频率为50.67，每阶频率间隔大于1Hz，频率分布合理。第二阶模态解耦率由70.22%提高到了97.31%；第三阶模态解耦率由63.46%提高到了98.14%；第五阶模态解耦率为43.27%提高到了93.96%；第六阶模态解耦率为56.24%提高到了95.64%。每阶模态解耦率均大于90%，系统振动耦合程度较低，优化效果显著。

4 结论

    (1)利用MotionView建立电动汽车动力总成悬置系统六自由度刚体模型，MotionSolve对动力总成悬置系统进行模态解耦率计算。计算结果表明，固有频率间隔较小，模态解耦程度较低。

    (2)以悬置安装位置和刚度为设计变量，固有频率为约束条件，模态解耦率为优化目标利用HyperStudy模块采用多目标遗传算法对悬置系统进行优化。优化结果表明，固有频率分布合理，有效的提高了模态解耦率。

    (3)利用MotionView/MotionSolve/HyperStudy可以对动力总成悬置解耦进行优化，为悬置系统设计提供有效的指导意见，缩短开发周期。