0 引言
随着现代工业的发展,对石油、天然气、煤炭等化石燃料资源的需求量不断提高,加上陆地资源的不合理开发与资源浪费,陆上资源逐渐枯竭。海洋蕴藏着储量惊人的石油、可燃冰等自然资源,近年来已经成为世界各国的开发重点。我国海洋面积广阔,特别是南海大陆架的石油、天然气资源,而海上资源的勘探与开采难度较高,因此,海上船舶与作业平台的精确定位具有重要的意义。
传统船舶采用锚泊的定位方式,这种方式需要非常长的锚链,在定位的时候会产生船舶绕锚点的周向运动,且易受到海浪、洋流等干扰。因此,传统的锚泊式定位难以满足现代远洋与深海的船舶精确定位方式。采用动力定位的船舶可以根据外界海浪、海风等干扰力,灵活的调节船舶周围推进器的作用力,从而使船舶保持动态平衡,实现精确的海上定位。
本文首先介绍了传统的船舶动力定位控制器,建立了简化的船舶动力定位数学模型和干扰力模型,并针对船舶动力定位控制器进行响应时间和响应速度的仿真试验。
1 船舶动力定位控制器系统的研究
控制器是船舶动力定位系统的“大脑”,控制器的性能直接决定了船舶动力定位的精度和效率。传统的动力定位系统采用PID控制器。
PID控制是一种最基础的控制方法,这种控制器的原理简单,同时具有灵活性高、故障率低等优点。图1为PID控制器的原理图。
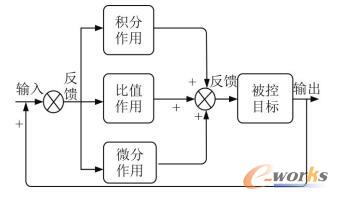
图1 PID控制器原理图
如图所示,PID控制器主要包括3个控制环节,积分环节、比例环节和微分环节,PID控制器将输出结果反馈到各个控制环节,从而提高控制精度。
船舶动力系统的PID控制器接收来自船舶传感器网络采集的海浪、海风、洋流等信号,信号过滤后进入比例环节、微分环节和积分环节,最终输出控制信号,调节船舶推进器的工作状态。
2 船舶动力定位系统的数学建模与定位控制器的仿真研究
2.1 船舶动力定位的运动建模
对船舶进行运动建模可以获取参数化的船舶运动模型,有利于提高动力定位控制器的控制精度。本文在建立船舶动力定位的运动模型时,分别建立了静坐标系O-XYZ和运动坐标系o-xyz下的模型。
船舶定位运动的静坐标系和运动坐标系下的运动模型如图2所示。
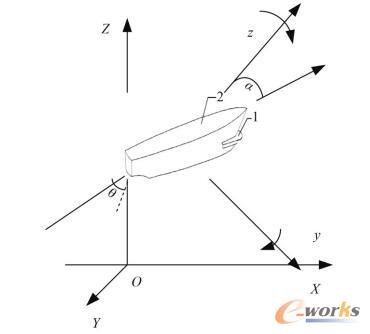
图2 船舶定位运动的静、运动坐标系下的运动模型
根据船舶动力定位过程的位移与旋转运动,本文在建立定位运动模型时分别建立了静坐标系下的沿XYZ三个轴的位移向量:s=(X,Y,Z)T和运动坐标系下沿xyz轴的速度向量:η=(u,v,r)T,船舶定位过程的作用力(静坐标系)如下式:
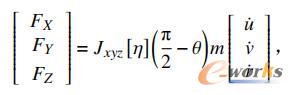
式中,Jxyz为船舶的转动惯量简化量,静坐标系与运动坐标系转换关系为:

式中:α为2个坐标系的空间转换角度;Vc为船舶相对运动速度。船舶在静坐标系中的运动模型:
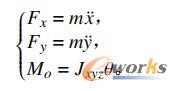
式中:Jxyz为船舶的转动惯量简化量;θ为船舶在定位运动的航向角。
2.2 船舶定位控制器的设计与仿真模型的设计
本文在船舶动力定位模型的基础上设计了一种非线性控制器,控制器模型主要在Matlab建立。
Matlab软件是一种专业的算法开发、数据分析和数值计算等功能的软件环境,广泛应用于各种控制仿真、建模等领域。
本文首先建立了海浪的运动方程为:
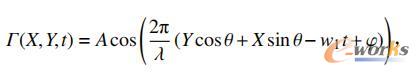
式中:λ为海浪的波长;θ为海浪的平均倾角;w1为海浪的频率;ψ为海浪作用于船舶的初始相角。
船舶定位过程中的海浪作用力为:
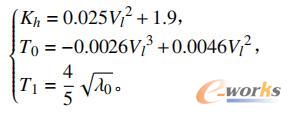
式中:Kh为海浪高;Vl为海浪流速;T0和T1为波浪的理论作用力和简化作用力。
船舶动力定位系统的控制器需要对多个输入量进行采集与分析,主要包括海浪、洋流、初始航向等,输出动力分配、船舶舵角等信号,从而控制船舶的动态平衡。
本文在Matlab中建立动力定位控制器的线性模型为:
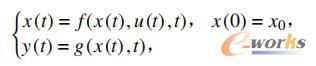
其中:x为控制器的输入量参数;f(t)和g(t)为x的变化函数。
该非线性系统的多个输入量可以表示为:
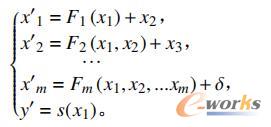
式中:Fm为舵角的控制函数;δ为非线性误差。
船舶动力定位控制器在采集信号时,由于外界环境和传感器自身的原因,会使采集的信号产生一些噪声信号,噪声离散信号如下式:
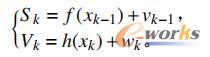
其中,函数f(x)和h(x)为均为非线性噪声干扰信号。
本文在Matlab中建立了相应的噪声过滤器,过滤器的函数模型如下:
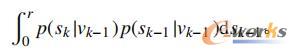
船舶动力定位系统的控制器仿真试验时,采用的船舶部分参数如表1所示。在Matlab中将控制器模型与船舶模型输入,设定一个初始位置和速度,可以获得船舶动力定位在一定时间的位移变化曲线如图3所示。
表1 试验用船舶模型的参数

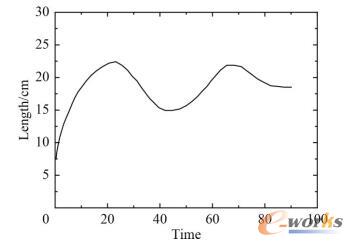
图3 船舶动力定位的位移仿真曲线图
3 结语
本文在传统船舶动力定位PID控制器的基础上,设计了一种基于运动模型的动力定位控制器,并在Matlab中对该控制器的控制精度进行了仿真试验。结果表明,该船舶动力定位控制器的控制精度在0.5m以内,具有较高的控制精度。
本文来源于互联网,e-works本着传播知识、有益学习和研究的目的进行的转载,为网友免费提供,并以尽力标明作者与出处,如有著作权人或出版方提出异议,本站将立即删除。如果您对文章转载有任何疑问请告之我们,以便我们及时纠正。联系方式:editor@e-works.net.cn tel:027-87592219/20/21。