本文对某款发动机附件支架进行结构优化设计。首先对支架安装基础模型进行缩减,然后基于缩减矩阵以及制造工艺需求,对支架进行拓扑优化设计,最终获得高性能、低成本的零件设计方案。既保留了完整的系统结构获取精确设计,又减小计算量节约计算时间,在工程开发中具有较高的应用价值。
1 前言
汽车发动机的附件(如发电机、空压机、转向泵等)较多,且位于发动机外围,各附件的正常工作对发动机性能有很大影响。依据发动机设计的布置需求,发动机附件一般通过其支架连接安装在发动机上,因此附件支架的设计是发动机设计开发的重要内容[1]。目前针对降低零件制造成本及提高整车燃油经济性的设计开发要求,通过对零件进行结构优化设计,可达到减重降本同时满足发动机开发性能的双重目的。
某款发动机的发电机支架在有限元分析时,发现模态较低,无法满足设计要求,决定采用结构优化方法重新对支架进行设计。若忽略安装基础模型的影响,仅对支架优化分析,则优化的支架不是满足发动机性能的最佳方案。本文首先采用“子结构法”对该发动机的发电机支架的安装基础模型进行缩减,获得模型的刚度矩阵和质量矩阵,然后导入缩减矩阵,并综合考虑制造工艺需求,对附件支架进行拓扑优化设计,最终对拓扑结果提取并重设计,获得满足发动机性能要求的设计结构。该方法不仅大大降低了开发周期和成本,同时获得高性能、轻量化的支架结构,在工程开发中具有较高的应用价值。
2 模型有限元分析
根据发电机的安装特点,有限元分析模型包含缸体、正时罩盖、简化发电机(确保发电机质量及质心位置与实际相符)、发电机支架、油底壳等。对系统进行模态分析,一阶频率207Hz,支架的原设计方案如图1所示,发电机支架重0.76Kg,模态分析结果如图2所示。

图1 支架原设计方案
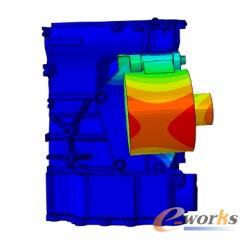
图2 原方案一阶频率振型图
3 基础模型缩减
众所周知,对发动机附件支架进行有限元仿真时,完整的对附件系统进行分析才能得到更准确的设计。然而优化计算是不断迭代寻优的过程,求解时间较长,因此在求解过程中,既希望保留完整的系统结构获取精确设计,又希望减小计算量节约计算时间。
“子结构法”就是将一组单元用矩阵凝聚为一个单元的过程,这个单一的矩阵单元称为“超单元”,使用“子结构法”可以节约计算时间,在有限的计算资源基础上求解大规模问题。比如静态缩减即把模型分为O集和A集(O集为缩减的集合,A集为保留的集合),形成静态方程:
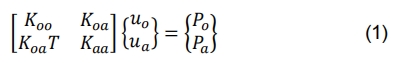
假设Po为零,使用ua求解uo,得
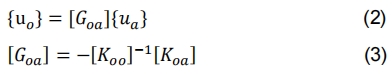
将(3)代入(1)中,得缩聚振动方程,缩聚后的刚度矩阵表达式为:
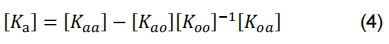
对发电机支架进行优化分析时,安装该支架的缸体、正时罩盖、油底壳等基础模型为支架提供刚度,但并不参与支架的优化迭代,因此可对这些基础模型进行缩减。缩减过程中与支架相连的螺栓安装点作为保留的集合A,其余为缩减的集合O。缩减模型如图3所示。
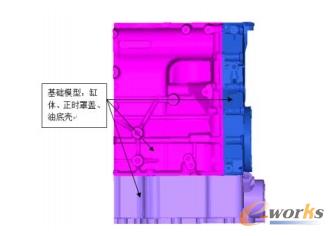
图3 基础缩减模型
缩减后得到**_AX.pch文件,默认情况下,刚度矩阵名称为KAAX,质量矩阵名称为MAAX,载荷矩阵名称为PAX。
4 支架拓扑优化
拓扑优化属于概念设计,在材料可布置的设计空间内通过寻优迭代计算获得材料的最佳布局。优化模型包括支架设计空间和发动机附件(为减少优化计算量附件被简化为质量点),如图4所示。其中红色部分螺栓安装孔,在优化过程中保持不变,作为非设计域,蓝色部分在优化过程中不断改变直到满足设计要求,作为设计域。

图4 优化设计空间
该优化模型的数学表达为:
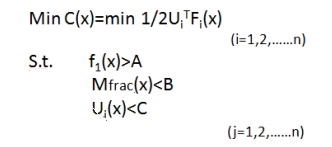
其中:x---设计变量;C(x)---目标函数;uiT---位移矩阵转置;Fi---载荷;f1(x)---第一阶固有频率;Mfrac(x)---优化后质量/设计空间质量;Uj(x)---附件载荷产生的位移。
优化技术得到推广还需要考虑制造加工性,如果现有工艺条件下不能被加工,或加工成本很高的优化结果,没有任何实用价值[2]。因此在优化中还考虑了制造工艺的约束,包括控制拓扑结构的成员尺寸大小,支架双向脱模等。导入缩减矩阵文件,保证系统刚度和质量在优化过程中不改变,综合以上对支架优化的众多考虑因素,对设计空间进行拓扑优化[3],经过43步迭代计算,优化模型收敛,单元密度阀值取0.3,优化结果如图5所示。

图5 拓扑优化结果
5 拓扑优化结果
优化结果虽是满足设计要求的最佳材料分布,但不能直接用于加工制造,工程师需要提取该优化结果同时结合工艺铸造要求进行二次设计建模。二次设计后的支架模型如图6所示,支架约重0.68Kg。
对该计算进行对比,采用“子结构法”优化计算时长约为完整模型优化时长的六分之一。

图6 二次设计支架方案
5 优化支架分析验证
直接把二次设计的支架方案替换原分析模型中的支架方案进行分析验证,系统一阶频率241Hz,如图7所示。优化方案相比原方案支架一阶频率提高了16.4%,而重量降低了10.5%。

图7 优化方案一阶模态振型
6 结论
本文从降低设计开发成本与提高产品性能两方面考虑,对某支架进行基于模型缩减的拓扑优化分析,分析结论如下:
(1)对模型进行缩减,获得系统的刚度矩阵和质量矩阵,可大大节约计算资源,同时保证系统分析的准确性;
(2)对关注零部件进行优化设计,可以快速、有效的为设计师提供满足各项性能指标的设计思路;
(3)通过优化设计,优化后的支架设计方案相比原方案,一阶频率提高了16.4%,而重量降低了10.5%。该设计思路不仅有效减少重复设计、验证次数,大幅缩短产品开发周期,而且获得性能较高的设计方案,在工程应用中起到很好的指导作用。
7 参考文献
[1]唐燕辉.发动机附件支架有限元分析及结构优化设计.《南京理工大学》2012年.
[2]张胜兰,郑冬黎,郝琪,等.基于HyperWorks的结构优化设计技术.机械工业出版社,2007:173-183.
[3]OptiStruct User,s Guide. Altair Engineering, Inc.
本文来源于互联网,e-works本着传播知识、有益学习和研究的目的进行的转载,为网友免费提供,并以尽力标明作者与出处,如有著作权人或出版方提出异议,本站将立即删除。如果您对文章转载有任何疑问请告之我们,以便我们及时纠正。联系方式:editor@e-works.net.cn tel:027-87592219/20/21。