大数据时代、信息化时代、网络化时代、智能化时代,也是系统时代。认识系统复杂性与调控复杂系统是当今科学技术发展的前沿。大数据一般来自具有各种反馈回路的复杂动态系统,既反映了系统性质或功能,也为进一步优化或调控系统服务;信息化与网络化使得系统组成部分之间的关联发生深刻变化,深刻影响系统的结构和功能;学习与反馈是智能化的两个核心机制,也是系统控制科学中处理不确定性的主要机制。这些研究都离不开对动态系统的定量认识与科学调控。因此,系统控制是关键基础。
1. 两位历史人物
1.1 维纳与《控制论》
诺伯特·维纳(N. Wiener),控制论的创始人,1894年出生于美国密苏里州,以其在数学与控制论等领域的开创性工作而闻名。1906年,仅12岁便进入塔夫茨大学数学系学习,而后于1912年,18岁时获得哈佛大学的博士学位;1932年,维纳成为麻省理工学院(MIT)的正教授;1933年,39岁当选美国国家科学院院士。1935至1936年间,维纳应邀访问中国,在清华大学与电机系的李郁荣教授合作,并在数学系讲学。维纳曾经把他在中国的这一年作为自己学术生涯中一个特定的转折点。在此期间,维纳还曾影响和指导过当时在清华大学工作的华罗庚,并在给英国著名数学家哈代(Hardy)的推荐信中称赞华罗庚是“中国的拉马努扬 (Ramanujan) ”。
维纳的学术贡献卓著,1964年维纳获“美国国家科学奖章”的授奖词比较全面的概括了其主要贡献:“在纯粹数学和应用数学方面并且勇于深入到工程和生物科学中去的多种令人惊异的贡献及在这些领域中具有深远意义的开创性工作”。科学文献中有许多以维纳命名的重要概念和成果,比如,维纳过程,维纳测度,维纳滤波,维纳-霍普夫方程等。
维纳最具影响力的成就是创立了控制论这一跨学科理论框架。他的里程碑式著作《控制论:或关于在动物和机器中控制和通信的科学》(Cybernetics or Control and Communication in the Animal and the Machine, 1948)[1],不仅开创了控制论这一新兴交叉领域,而且对计算机、人工智能、通信理论、控制理论、自动化、心理学、认知科学、生物学、经济学与管理学等众多领域产生了深远影响。继《控制论》之后,1950年维纳在其姊妹篇《人有人的用处》[2]中进一步拓展了对控制论和信息论的哲学与社会学反思,提出了对科技、社会和人类未来深刻的见解,在普及和发展控制论方面发挥了重要作用。
《控制论》受二战影响和学科交叉而诞生,它有几个来源,涉及计算机设计,防空火炮工作,通信与信息,以及神经生理学等 。全书共10章,密切围绕 “控制与通信” 这条主线以及 “反馈” 这一基本原理,从 “动物智能” 与 “机器智能” 的若干重要方面展开对比讨论, 并认为 “智能的首要问题是‘学习’”。毫无疑问,控制论与智能系统之间具有深刻的关联。
维纳试图建立控制论的统计理论,但他认为吉布斯 (W. Gibbs) 的统计力学是不能直接用来研究控制系统的,因为“一个控制系统不是一个孤立的系统,而是一个与周围环境密切联系的系统,特别是控制系统通过自身的反馈机构可以减少系统的‘无组织程度’,因此,在控制系统中经常发生熵减少的过程”。
诺伯特·维纳创新性的提出了关于平稳随机过程的预测和滤波的理论,并对信息论产生了重要影响。维纳指出:“正如一个系统中的信息量是它的组织化程度的度量,一个系统的熵就是它的无组织程度的度量;二者互为正负对立”。他还强调:“信息就是信息,不是物质也不是能量”。维纳对克劳德·香农 (C.Shannon) 的信息论也产生过重要影响,香农在他的著名论文《通信的数学理论》[3]中提到:“通信理论在其基本哲学和理论上深受维纳的影响”。香农在这篇文章中还提到:“维纳对平稳过程的滤波和预测问题的优雅解决方案,对我在这一领域的思考产生了相当大的影响。”
控制论(Cybernetics)的影响远不止上述这些,实际上对当今众多科学技术与社会科学领域都产生了广泛影响。书中的思想洞见对当今系统控制与智能系统的进一步发展仍具有重要意义。此外,赛博(Cyber)语言在当今也广泛流行(如cyber-space, cyber-security, cyber-culture, cyber-game, cyber-physical system, ……)。维纳堪称交叉科学研究的典范!
控制论的创立无疑是划时代的,很快从美国传播到世界。上世纪五六十年代《控制论》在苏联曾经历过被“批判-平反-热捧”过程,曾得到同时代的数学家A.N.科尔莫戈洛夫、S.L.索波列夫、A.A.李雅普诺夫、A.A.马尔科夫(Jr.)等积极支持[4]。维纳《控制论》中文版于1961年出版,翻译者的署名是“郝季仁”(“好几人”的谐音,实际上是龚育之、罗劲柏、侯德彭、陈步四人),这个署名是一段历史的产物。
1.2 钱学森与系统控制
钱学森(1911.12.11-2009.10.31),一位在我国家喻户晓的杰出科学家,其科学生涯纵贯70年,可以认为横跨了三个非凡的时期。
第一个时期是20世纪30年代中到50年代中在美国的20年,钱学森以其出众的才华成为那个时代科技前沿的著名专家,特别是在空气动力学研究方面提出了亚音速气流中空气的压缩性对翼型压强分布的修正公式(“卡门-钱学森公式”),并为美国的航空和火箭技术发展做出重要贡献。在他回国之前被限制自由的五年期间,撰写了《工程控制论》。
钱学森在《工程控制论》[5] 中提出“工程控制论是一门技术科学,它不同于工程实践”,“工程控制论的目的是研究控制论这门科学中能够直接用在工程上设计被控系统或被操纵系统的那些部分”,“控制论所讨论的主要问题是一个系统的各个不同部分之间的相互作用的定性性质,以及整个系统总的运动状态”。这本经典著作于1956年被翻译成俄文出版,1957年被翻译成德文出版,1958年被翻译成中文出版。1980年,钱学森与宋健出版了《工程控制论》的修订版,扩充了原著的内容。在修订版的序言中,作者进一步阐述了现代化、技术革命与控制论的关系,指出“从科学理论的角度来看,20世纪上半叶的三大伟绩是相对论、量子论和控制论”,并指出核能技术革命、计算机技术革命和航天技术革命等 “所有这些技术革命都直接与控制论连在一起”。
第二个时期是1955回到祖国至1978年,钱学森投身到“两弹一星”工程中,成为中国航天事业的奠基人,后来被授予“国家杰出贡献科学家”和“两弹一星功勋奖章”等。1978年9月27日钱学森、许国志与王寿云在《文汇报》发表文章“组织管理的技术——系统工程”,这篇里程碑式文章在我国产生广泛而又深远的影响。钱学森身体力行,大力推动我国系统工程的发展、普及和传播,在这方面做出了开创性贡献。时至今日,“系统工程”概念在我国现代化建设工作中已经深入人心,经常在重要政策文件和各级领导讲话中被提到。
第三个时期是我国改革开放快速发展的30年,钱学森紧密结合我国现代化建设实际问题,重点研究开放的复杂巨系统理论,致力于创建系统学。1991年,钱学森、戴汝为、于景元在《自然》杂志发表题为“一个科学新领域——开放的复杂巨系统及其方法论”的著名文章,先后提出“从定性到定量的综合集成研讨厅体系”与“大成智慧工程”等概念与方法论。这一时期钱学森对复杂巨系统的研究与探索工作集中反映在《创建系统学》[6]一书中,大大推动了中国复杂系统的研究,对我国系统科学发展产生了深远影响。
值得提及的是,在钱学森的倡导下,经中国科学院和国防部第五研究院商定,于1962年在中国科学院数学研究所成立了控制理论研究室,数学所的关肇直和五院的宋健分别担任研究室的正副主任,该室是我国最早从事现代控制理论研究的科研机构。1979年该室成为国务院新批准成立的中国科学院系统科学所的控制理论研究室(关肇直先生担任系统科学所的首任所长)。这个研究室就是今天中国科学院系统控制重点实验室的前身。令人感动的是,钱学森先生在逝世的一周前,还写信祝贺中国科学院系统科学所成立30周年,鼓励大家继续为发展系统科学做贡献。
2. 几个基本概念
2.1 系统与系统科学
系统是自然界和人类社会中一切事物存在的基本形式,各式各样的系统组成了我们所在的世界。现代科学在从基本粒子到宇宙的不同时空尺度上研究各类具体系统的结构与功能关系,逐渐形成了自然科学与社会科学的各门具体科学。
什么是系统?通常来讲,一个系统是由相互关联和相互作用的多个部分(或子系统)所组成的具有特定功能的有机整体,这个系统又可作为子系统成为更大系统的组成部分。
系统科学研究什么?系统科学的研究对象是“系统”自身,其目的是探索各类系统的结构、环境与功能的普适关系以及演化、认知与调控的一般规律。
钱学森曾经提出系统科学的体系结构,包含四个层次:
第一个层次是哲学层次,称为系统论。值得注意的是,系统论不等于整体论。钱学森认为系统论是还原论与整体论的辩证统一,这个观点很精辟。正是这种辩证统一,使得系统论既可以超越还原论,又可以超越整体论。
第二个层次是基础理论,称之为系统学(Systematology)。这个英文单词是钱学森先生给出的,他认为系统学是系统科学的基础理论,有待建立。
第三个层次是技术科学,包括运筹学、控制论、信息论等内容。
第四个层次是工程技术,包括系统工程、通信工程、自动调节原理等。
为了进一步理清系统学的基本内涵和重要意义,本人在2016年发表了一篇兼具科普性与探索性的文章《系统学是什么》[7],讨论了系统科学的产生背景、意义作用、时代挑战与发展基础,特别是提出了系统学的体系结构,包括“五论”:系统方法论、系统演化论、系统认知论、系统调控论、系统实践论,并且还探索了关于“系统复杂性”的定义。本人认为,“系统复杂性”不同于计算复杂性等通常所说的复杂性定义,应该体现系统概念的内涵。
2.2 系统的控制
我们从事科研活动的目的,不仅要认识世界,还要改造世界。系统控制的目的是通过对系统施加一定影响,改变其运动状态,以实现系统预定目标。在我们日常工作和生活中,有许多与控制概念相似、相近或相关的概念,如调控、调整、调节、校正;指挥、支配、操纵、驾驭;管理、管制、抑制、约束;决策、调度、规划、优化等。控制概念广泛应用于自然科学、工程技术、经济管理、社会治理与生态环境等领域,如温度控制、导弹控制、飞机控制、汽车控制、经济调控、污染控制、环境调控等等。
2.3 前馈与反馈
在控制系统中,前馈与反馈是两种基本的控制策略。前馈一般是基于对可能影响系统演化因素的先验信息或基于对系统未来演化态势的预测而提前采取的调控措施,可以分为正前馈和负前馈。反馈则不必事先知道影响系统演化的不确定性因素的确切来源和具体大小,主要根据系统实时运行中所反映出的信息观测来调整系统未来的演化行为,分为正反馈和负反馈。前馈与反馈的作用是互补的,两者的有机结合是对不确定性动态系统进行有效调控的基本策略。
显而易见,数字化、网络化与智能化技术的迅猛发展,既可以增强我们设计前馈策略的能力(如借助强化学习等),也可以增强反馈策略的实施效果(比如通过增大反馈信息量与加快反馈速度等)。进一步,对复杂系统的调控来讲,正反馈(前馈)与负反馈(前馈)策略也具有互补的功能,但通常需要两者的协调与平衡。由于反馈具有应对不确定性因素影响并不断改进系统性能的突出能力,因而是控制系统中最核心的概念。正如维纳所言,反馈无处不在,体现在几乎所有有目的的行为中;钱学森同样认为,反馈是工程控制论的一个最主要的概念(目前在工程系统中大多采用负反馈)。
总的来说,反馈是一条基本的系统学原理,可以产生有序行为,维持系统稳定或平衡,以及应对各种不确定性因素影响以达到控制目的。除此之外,反馈机制在智能行为及系统进化中起着关键作用,反馈控制算法是自动化和智能化系统“大脑”的核心组成部分,反馈控制也被认为是第一个系统学科[8]。从历史上看,正如国际著名控制科学家K.J. Astrom所指出的,反馈的有效利用常常对工程技术领域产生革命性影响。
下面举一些典型例子来说明反馈机制的重要作用。
3. 反馈系统的若干实际例子
例1. 瓦特蒸汽机
我们讲的第一个著名例子是瓦特蒸汽机。1782年,詹姆斯·瓦特(J. Watt)在前人工作基础上创新性发明将 “离心调速器”用于反馈控制蒸汽机的速度,以应对负载的变化。这一发明促进了蒸汽机的广泛应用,成为英国工业革命的一个重要标志。离心调速器的反馈工作原理可以简单描述如下 (见示意图):当蒸汽机运转过快时,竖轴转速增加,导致两个金属小球在离心力作用下升高。因为小球通过连杆与蒸汽阀门相连,小球的升高会使阀门关小,从而降低蒸汽机的转速。相反,如果蒸汽机转速过慢,小球则下降,连杆随之将阀门开大,从而使蒸汽机转速变快。
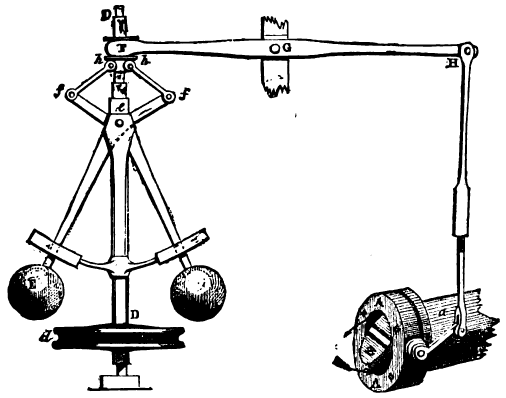
图1
尽管调速器的引入最初改善了蒸汽机的运行稳定性,但随着蒸汽机速度的提高,系统开始出现震荡,暴露了调速器设计的问题,这也促使了后续关于调速器和系统稳定性的理论研究。著名的电磁场理论创立者、英国物理学家詹姆斯·克拉克·麦克斯韦(James Clerk Maxwell,1831-1879)是最早研究调速器稳定性问题的学者。他在1868年发表的《论调节器》中首次用微分方程来描述调速器的运动状态,并对其在平衡点附近进行线性化处理,指出了稳定性取决于特征方程的根是否具有负实部。麦克斯韦被认为是历史上第一个控制理论学家。维纳在他的《控制论》一书的引言中曾提到,选择Cybernetics这个字是想用它来纪念关于反馈机构的第一篇重要论文,就是上面说的麦克斯韦这篇论文。麦克斯韦之后,关于系统稳定性的研究工作先后出现了Routh-Hurwitz判据、Lyapunov稳定性理论和Kharitonov定理等重要理论进展,进一步推动了控制理论的发展。
例2. 远距离通讯
另一个著名例子是远距离通讯。在20世纪30年代,贝尔电话实验室的电气工程师H.S. Black的反馈放大器发明为远距离通讯技术作出了关键性的贡献。由于电信号在远距离传输过程中会逐渐衰减,需要依靠放大器来增强信号。然而,放大器的非线性特性会导致信号失真,并且随着信号的放大,噪声和失真也会被放大。1921年时通信的最远距离不超过1000英里。Black在1921年开始研究放大器的相关问题,并于1928年8月8日提交了负反馈放大器的发明专利。这种设计通过选取适当小的负反馈系数(-β>0)和充分大的放大倍数(μ)来实现信号的有效放大,同时大幅度减少噪声和失真。显然,这是关于反馈机制的一个十分巧妙的运用!然而,这一专利直到1937年12月21日,即提交申请后的九年多之后,才被正式批准。
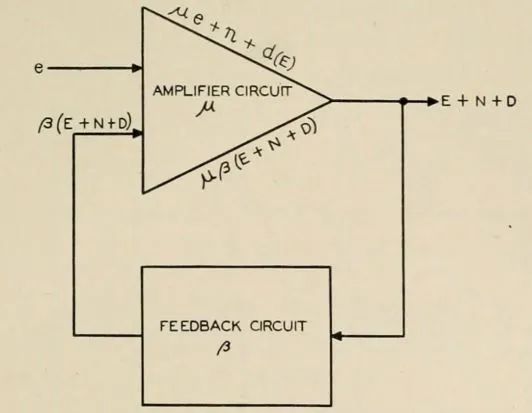
图2
这项发明的重要性曾被美国贝尔实验室的研究主任M.B. Kelley高度评价,他在1957年曾指出:“毫不夸张地讲,若没有Black发明的反馈放大器,今天我们所见的覆盖全国的长途电话和电视网络以及越洋电话电缆将不存在”。Black的这一工作推动了经典控制论中的频域方法研究,后来发展出了Nyquist判据、Bode图、以及Evens根轨迹等著名方法,成为经典自动控制理论的重要内容。
例3. STM与高性能探测器/观测器
我要提的第三个关于反馈原理应用的例子是扫描隧道显微镜(STM),由IBM公司的科学家G. Binning和H. Rohrer于1981年根据量子力学中的隧道效应发明,获1986年诺贝尔物理学奖。基本原理是利用隧道电流来反馈控制针尖在样品表面的精细扫描。STM的诞生标志着人类第一次能够实时观测原子在物质表面的排列以及研究与表面电子行为相关的物理化学性质。通过精密控制STM的针尖,可实现对原子和分子的移动和操纵,为纳米科技的发展奠定了坚实的基础。随后发展的原子力显微镜(AFM)也离不开反馈控制系统。此外,近期与反馈控制密切相关的诺贝尔奖成果还包括了2017年获奖的引力波探测和2020年获奖的黑洞观测。这些研究工作都展示了反馈原理在现代科学技术中的重要作用和广泛影响。
例4. 阿波罗登月
1969年阿波罗登月计划的最终成功,是我要提及的第四个关于系统控制重要作用的突出实例。在这一里程碑式的重大工程任务中,火箭的上升阶段应用了最优控制算法,而在飞行轨道的修正方面则应用了卡尔曼滤波算法。关于数学算法在这项举世瞩目的重大工程中的重要性,1988年美国工业与应用数学学会 (SIAM) 发布的“控制理论未来方向”研究报告[9]中,有下列一段评述,给人留下深刻印象:“非常普遍地,一片计算机芯片被看作是科学突破,而人们往往忽略了芯片的‘大脑’实际上是数学算法。以阿波罗登月任务为例,许多人强调舱载数字式飞行计算机的关键作用,却忽视了存储在内存中的创新数学算法对任务成功的同等重要性。” 这段话强调了数学算法在这一航天重大科技成就中的重要作用。
例5. 高机动性战斗机控制等
高机动性战斗机控制是系统控制发挥重要作用的又一显著领域。例如,在F-16战斗机中,传统的机械联动装置被先进的数字计算机和电线取代,形成遥控自动驾驶仪系统。这种系统设计有几个关键特点:1) 是开环不稳定设计:为了提升战斗机的机动性,F-16被设计成开环不稳定系统。这意味着在没有适当控制系统的情况下,飞行器本身是不稳定的。2) 数字式反馈控制系统:这个系统的反应速度很快,能够实时应对空气动力学的不确定性因素,并可以有效地镇定一个不稳定的动态系统。通过这种创新的控制方法,F-16战斗机能够在保持高度机动性的同时,确保飞行的稳定性和安全性。这个例子展示了反馈控制技术对高性能飞行器的重要性。事实上,反馈系统在运动控制中起着关键作用的重要例子有很多,比如机器人,无人机,自动驾驶,......。
例6. 深海钻井平台的自动定位
控制系统在深海钻井平台的自动定位中发挥关键作用。以我国“海洋石油981”深水半潜式钻井平台为例,该平台在设计上充分考虑了南海恶劣的海洋环境,具备极强的稳定性和抗干扰性,能够在最大3000米的水深作业区域内稳定工作,可抗200年一遇超强台风。能做到这点,关键在于其八个分列四角的螺旋桨推进器,这些推进器通过控制系统进行实时自动定位调节,确保平台的稳定性和抗干扰能力。
例7. 生态系统的反馈调节
生态系统的稳定性和平衡依赖于其内部的自我调节机制,其中反馈机制起着至关重要的作用。在生态系统中,如果某一个成分发生了变化,它将必然引发系统内其他成分的一系列响应变化。这些响应变化最终会再次作用于最初发生变化的成分,形成一种自我调节的过程。生态学中著名的Lotka-Volterra方程就是这种现象的一个简单描述。
该方程用于描述两个物种之间的相互作用,特别是在被捕食者和捕食者之间的关系。它揭示了两个物种数量之间的竞争关系如何通过正负反馈机制相互影响。当一个物种的数量增加,可能会导致另一个物种数量的减少,反之亦然。这种动态平衡是生态系统自我调节的一个典型例子,显示了生态系统中复杂的相互依存和调节关系。
例8. 生理功能与反馈机理
反馈被认为是生命的核心特征。生物机体能够维持正常的生理功能,依赖于多种反馈调节机制,包括神经调节、体液调节以及局部的自身调节。这些调节机制在生物机体的各种组织、器官和系统中普遍存在,并且在分子、细胞和系统各个层面上都发挥着作用。精确的反馈调节对于机体的正常功能至关重要,如果缺乏这种反馈调节或其功能失效将导致各种疾病的发生。
2017年诺贝尔生理或医学奖的获得者就是因为“发现了调控昼夜节律的分子机制”而获奖。生物钟机制是一个典型的生物反馈调节系统,它调控着生物体内部的节律。虽然不同种生物的生物钟基因多种多样,但他们的工作原理都是类似地的,即基因表达的负反馈调节。此外,糖尿病就是生物机体反馈调节失衡的一个著名例子。胰腺通过产生胰岛素和胰高血糖素来调节血液中的葡萄糖水平。在糖尿病患者中,由于胰岛素的调节机制受损,导致血糖水平无法有效控制,从而引发了一系列健康问题。这再次说明了生物机体中精准的反馈调节对于维持生命健康的重要性。
例9. 中医理论
中医药在中华民族几千年的生存与发展中做出了巨大的贡献。中医理论是建立在功能结构模型基础上的理论体系,包括精气学说、阴阳五行、藏象学说、经络学说、体质学说、病因病机、辨证施治、三因制宜等概念,体现了丰富的整体思维、辩证思维、唯象思维以及功能建模等系统方法。这一理论体系蕴含着深刻的系统演化论、系统认知论和系统调控论的思想。特别是“阴阳平衡”原则,它不仅是理解生理功能、解释病理变化的核心,也是指导疾病诊断和治疗的关键。反馈调节是保持人体“稳态”的基本机制。在中医药现代化的进程中,系统控制科学有望在其中发挥更加重要的作用。系统控制不仅有助于更深层次地理解中医药的内在机理,还可能推动中医药与现代科技的融合,从而促进这一传统医学体系的发展和创新。
例10. 市场经济及调控
1776年英国的亚当·斯密(1723~1790)首次发表了《国民财富的性质和原因的研究》(简称《国富论》),书中所论述的那只在暗中推动市场经济行为的“看不见的手”,其工作原理也属于反馈机制。它通过价格波动自动调节市场上商品的种类与数量以达到供需平衡,这一“自组织”原理至今仍在深刻影响着全世界经济发展。此外, 政府的宏观调控在本质上也是利用正负反馈原理。当今,在社会尺度上有大量挑战性问题需要系统控制的研究[10]。
反馈控制成功的应用例子数不胜数,近期相关的还可参见[11]。
总之,反馈机制在自然科学、工程技术、经济社会和生态环境等领域无处不在、无时不有。尽管反馈有许多突出优点,但也有不足之处[12]。比如,如果设计不当的话,可能导致被控系统的不稳定。人们自然关心如下基本科学问题: 如何有效利用反馈?如何具体设计反馈规律?如何分析预测反馈系统性能?如何使被控系统达到期望目标?反馈机制的最大能力和根本局限是什么?为了解决这些问题,需要研究系统控制理论与设计方法。
4. 主要设计方法概述
下面是关于控制系统的一个一般性框图 :
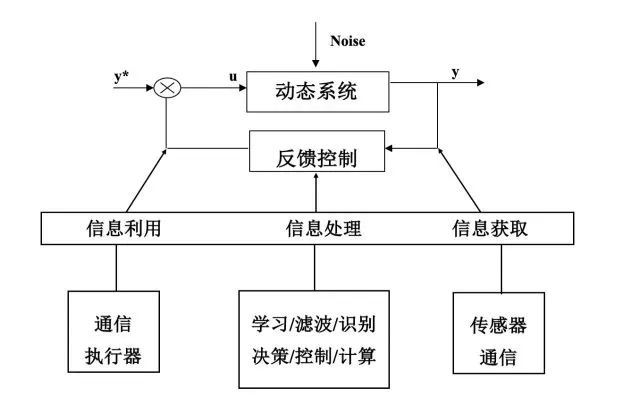
图3
从图中可以看出,控制系统与感知、信息、通信、学习、优化、计算等都是密切相关的,在这些重要环节上的技术进步, 都可能推动控制器设计方法与控制系统整体性能的进步和提升。下面将主要集中于控制器设计中的一些主要设计思路或方法的简单介绍。
图4
在经典控制论中,最著名的反馈控制方法当属下面的“比例-积分-微分(PID)控制”:
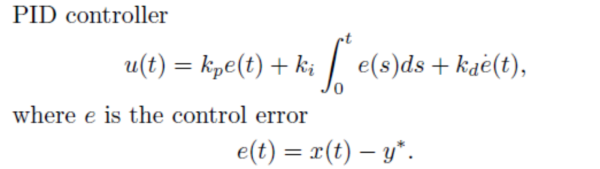
图5
在被控的动态系统中有控制输入信号和观测输出信号,通过观测输出信号和理想目标之间的运行偏差来决定反馈控制信号,它是由运行偏差的比例、积分、微分这三项的线性组合来决定,称为PID控制。
PID控制虽然有上百年历史,但因为其不依赖具体数学模型,具有简单性、实用性和鲁棒性等突出的优点,在当今工程技术系统的控制器设计中仍占据主导地位。事实上,据统计,“90%以上的工业控制问题是采用PID解决的”。控制系统被视为自动化系统的“大脑”,而自动化技术又是将人类从繁重的体力和脑力劳动中解放出来的关键技术之一,对生产力的发展起着重要推动作用。因此,有人认为“没有PID,就没有现代文明”,这在一定程度上反映了PID控制在现代技术社会中的重要性和广泛影响。
正因为如此, 对PID控制器的基础理论与参数设计方法的科学研究一直持续不断。但直到前不久[13],才从数学理论上严格证明了线性PID控制可以应对大范围非线性不确定性动态系统,并且证明了PID闭环控制系统无论对非线性函数的不确定性还是对控制器中三个关键参数的设计选取,都具有大范围鲁棒性(称为“双边鲁棒性”),从而说明了PID为何在实际应用中如此成功的基本原理。
尽管PID控制器在工业中影响巨大,但也不是万能的,例如PID控制难以解决控制变量受约束下多输入多输出动态系统在一般性能指标下的优化控制问题。上世纪60年代前后,诞生了现代控制理论。其主要标志是基于状态空间方程的卡尔曼 (R.E. Kalman) 滤波,线性二次最优控制问题的求解与若干基本概念 (能控性、能观性、结构分解与最小实现等) 的引进和刻画,以及贝尔曼 (R. Bellman) 动态规划和庞特里雅金 (L.S. Pontryagin) 极大值原理等。
4.2 优化方法
优化方法可以定量设计信息反馈规律,保证系统稳定性与一般性能指标下的最优性,并且也可研究瞬态响应等。传统的最优控制需要精确数学模型,一些标志性成果包括线性二次型(LQ)控制、极大值原理、动态规划方法,以及近年来广受关注的模型预测控制(MPC)等。
关于最优控制理论,贝尔曼(Bellman)和庞特里雅金(Pontryagin)的工作,分别对连续时间Hamilton-Jacobi理论和古典变分学进行了拓展,为多输入多输出非线性动态系统在控制变量受约束的情况下,根据一般性能指标进行最优控制求解提供了一般性的数学理论指导。Pontryagin极大值原理在阿波罗登月等航天任务中得到成功应用,并且其随机情况的推广启发了一般非线性倒向随机微分方程(BSDE)的数学研究。此外,对Hamilton-Jacobi-Bellman动态规划方程的研究也导致了偏微分方程中粘性解(viscosity solution)概念的提出和使用。
然而,这些关于动态过程的优化控制方法一般依赖于精确的数学模型,因此在应用于实际中多数不确定性复杂系统时,存在基本的局限性。这激发了对不确定性动态系统控制的深入研究,并促进了许多新方向的发展。
对于不确定性系统的控制律设计,可大致分为三类方法[14]:一是基于先验知识和/或统计数据进行离线建模或学习,然后设计控制器,或直接从强化学习中学习控制规律(适用于可多次重复的情况)。二是直接利用闭环系统运行中的在线观测数据来设计反馈控制规律,无需具体的数学模型。三是前两者的有机结合。实际上,实践中成功的应用往往都是基于系统建模(或离线学习)与反馈控制的有机结合。
4.3 学习方法
通过学习可以为控制器设计提供所需的基本模型和状态信息。动力系统的学习问题可以包括系统辨识、状态估计、适应滤波、强化学习和反问题等。系统辨识方法一般要先选定一个含有未知参数的线性或非线性模型集,然后利用预报误差方法从模型集中选出最优的模型参数。信号滤波的目的则从含有噪音的信号过程中提取或者估计出所希望知道的信号。强化学习一般是指在动态系统的输入信号和运行状况可以多次重复的情形下,对控制规律的学习。系统辨识与强化学习大家都应该比较熟悉了。我这里仅谈一点关于滤波问题或运动状态估计问题。
1960年Kalman引进状态空间方法来描述非平稳随机过程,并将对观测数据的处理与系统的结构信息有机结合。结构信息可以用于离线求解非线性 Riccati方程,而对系统未来状态的估计和预测,仅利用当前的估计值和实时的输出观测值,形成关于系统未知状态的递推算法。Kalman滤波不但突破了Wiener滤波和Kolmogrov滤波只能处理平稳信号的局限,使得以递推方式求解(有限维)非平稳过程的滤波成为可能,可以节省在线计算时间和数据存储,从而很方便地处理“流数据”。Kalman滤波及其变形目前已经广泛应用于空间技术与军事、导航与制导、GPS定位、雷达跟踪、大气观测、水文建模、计量经济等领域。
4.4 鲁棒方法
任何数学模型在本质上都是对实际复杂系统的抽象或近似表示,数学方法的鲁棒性对于解决实际中的复杂系统问题是至关重要的。具体来讲,基于理想化模型(或标称模型)所设计的控制器在应用于不确定性实际系统时,可能面临模型与实际系统之间存在“较大”偏差的问题。如何确保这样的控制器能够有效控制那些与数学模型有显著差异的不确定性系统,是鲁棒控制研究的主要内容。这要求控制器不仅要在理想条件下表现良好,而且能够在面对系统不确定性或变化的实际环境时依然保持其稳定性和基本性能。目前,无论对线性系统还是非线性系统,关于鲁棒分析与鲁棒控制都有丰富的研究成果。
4.5 自适应方法
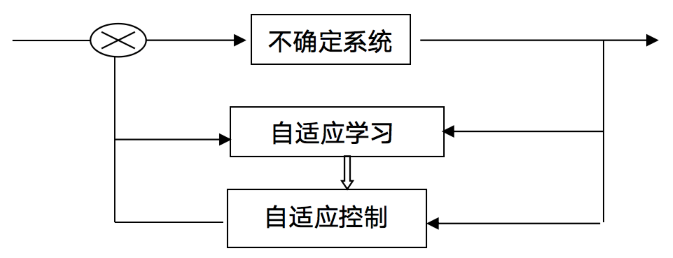
图6
自适应控制是一种基于在线自适应学习或自适应滤波来设计反馈控制器的方法,能够通过自适应学习而具备实时应对大范围不确定性的自适应能力。这种方法的核心在于将学习机制和控制规律融合在同一个反馈回路中,因此一般比鲁棒控制能够处理的不确定性范围要大很多。显而易见,自适应控制系统是一种基本的“认知-决策-行动”型一体化循环迭代智能系统,它的突出特点在于它将统计学、控制论和动力系统理论等进行了有机的融合,为处理复杂不确定性结构(参数)以及动态变化的系统环境提供了一种有效的策略。通过这种方法,控制系统能够根据环境变化和系统性能反馈实时调整其行为,从而在面对不断变化的实际条件时,保持高效和稳定的运作。从理论上讲,闭环自适应控制系统一般由很复杂的非线性随机动力学方程组所刻画,由其所决定和产生的动态系统的输入与输出信号是非平稳与强相关(远非独立)的数据流。这就给严格的理论研究带来很大挑战:要想系统被控制得好,需要在线学习的好;而要在线学习的好,需要系统的数据性质好;而系统的数据性质好,意味着系统要控制得好。这就回到了论证的起点,构成了一个数学证明中的所谓“循环论证”。在自适应系统理论研究中,如何跳出或避免这类“循环论证”,是理论研究的核心困难。
一个典型例子是著名的自校正调节器(STR),它是由线性随机动态系统的“最小二乘”学习算法与“最小方差”控制规律在线耦合而成的。毫无疑问,由这两个最基本的“最优原理”所产生的自校正调节器,不仅其构造自然美妙,而且具有基础性意义,是一类典型而又基本的“认知-决策-行动”型智能系统。进一步,无论模拟仿真还是实际应用,都表明它的确具有良好的控制性能。事实上,STR在自适应控制历史上具有里程碑意义,关于STR的研究曾经使得自适应控制领域在上世纪七十年代初开始得以复兴,从理论和应用两方面促进了自适应控制发展。然而,由于STR在本质上,是由一组很复杂的非线性与非平稳随机动力学方程组所刻画(即使被控对象是线性系统亦然),这就使得为其建立严格的稳定性与收敛性理论遇到预想不到的数学困难,曾经是控制理论中长期公开的研究难题,直到上世纪九十年代关于STR理论研究中的“循环论证”问题才得以解决。关于自校正调节器的更多研究历史和研究体会可以参考本人的《回溯自校正调节器研究之路》这篇文章[15]。
自适应方法还可以包括自抗扰控制(ADRC)与极值搜索控制(ESC)等,因为他们都利用了自适应在线估计器来设计反馈控制律。
4.6 更“智能化”方法
借助大数据与人工智能等信息技术的发展,通过离线学习、强化学习、自适应学习等方法与在线反馈机制的有机结合,充分发挥并有机融合前馈机制与反馈机制的不同优势和功能,处理更大不确定性、混杂性、稀疏性与不完全信息,特别是在博弈控制系统框架内研究具有博弈行为的多主体复杂系统的智能化调控或决策(涉及多主体、多层次、多目标、多约束、博弈性、自主性等)。需要人工智能、控制论、博弈论、动力系统乃至法学与伦理学等社会科学领域有关学科的深度结合。
以上只是简单概括了六大类控制规律的设计方法,在这里无法做到面面俱到,也不可能深入探究。本人与多位同事们共同完成的《控制理论导论》[16]一书可以为有兴趣深入了解相关内容者,提供部分参考。特别地,关于反馈机制与不确定性之间定量关系的深入研究,可以参考作者的文章[14]与[17]。此外,关于系统控制的有关内容与人才培养,至少涉及数学、系统科学、控制科学与工程等几个一级学科。
5. 新时代的展望
系统是任何事物存在的基本方式,也是人类认识世界和调控世界的基本概念。认识系统复杂性与调控复杂系统已成为当今科学技术发展的前沿。大数据时代、网络化时代、智能化时代,也是系统时代。事实上,大数据一般来自具有各种反馈回路的复杂动态系统,既反映了系统性质或功能,也为进一步优化或调控系统服务。信息化与网络化不但使得系统组成部分之间的关联发生深刻变化,深刻影响系统的结构和功能,并且造就了大量新的复杂系统。智能化的两个核心机制是学习与反馈,两者也是系统控制中处理不确定性的主要机制。所有这些问题的深入研究都离不开对动态系统的定量认识与科学调控。因此,系统控制科学仍是关键基础。
另一方面,数字化、网络化与智能化等信息技术的迅猛发展和广泛应用,在助力或赋能复杂系统控制研究和技术实现的同时,也造就了大量新的挑战性复杂系统控制问题需要研究解决。例如,“人机融合”或“信息-物理-社会”复杂系统的调控需求,将可能使传统系统控制科学的研究框架或研究范式面临变革。
回顾历史,系统控制思想与方法的应用遍及几乎所有科学技术领域,成就了现代人类文明之美。展望未来,迎接新时代的机遇与挑战,系统控制仍具有非凡的魅力,将助力我们促进新质生产力发展,建设更加美好的和谐社会,实现人类文明的持续发展!
参考文献
[1] Wiener N. Cybernetics: or Control and Communication in the Animal and the Machine. Cambridge: The MIT Press, 1948. [Wiener N, 著. 郝季仁, 译. 控制论: 或关于在动物和机器中控制和通信的科学. 北京: 北京大学出版社, 2007]
[2] Wiener N. The Human Use of Human Beings: Cybernetics and Society. Washington: Da Capo Press, 1954. [Wiener N, 著. 陈步, 译. 人有人的用处: 控制论与社会. 北京: 北京大学出版社, 2010]
[3] Shannon C.E. A mathematical theory of communication[J]. The Bell system technical journal, 1948, 27(3): 379-423.
[4] Slava Gerovitch. From newspeak to cyberspeak: a history of Soviet cybernetics. The MIT Press, London, England, 2002.
[5] Tsien H.S. Engineering Cybernetics. New York: McGraw-Hill Book, 1954. [钱学森, 著. 戴汝为, 何善堉, 译. 工程控制论. 上海: 上海交通大学出版社, 2007]
[6] 钱学森. 创建系统学. 上海: 上海交通大学出版社, 2007.
[7] 郭雷. 系统学是什么. 系统科学与数学. 2016, 36: 291–301. [Guo L. What is systematology. J Syst Sci Math Sci, 2016, 36: 291–301]
[8] Astrom K.J. and Kumar P.R. Control: A perspective, Automatica, 50, 3-43, 2014.
[9] Fleming W.H., et al. Future Directions in Control Theory: A Mathematical Perspective. SIAM, Philadelphia, 1988.
[10] Annaswamy A.M., Johansson K.H., and Pappas G. J.(eds.). Control for Societal-scale Challenges: Road Map 2030, IEEE Control Systems Society, 2023.
[11] Samad T. & Annaswamy, A.M. (eds.). The Impact of Control Technology, (Second Edition), 2014, Available at www.ieeecss.org.
[12] Astrom K.J. and Murray R.M. Feedback Systems: An Introduction for Scientists and Engineers. Princeton University Press, Princeton, 2008.
[13] Zhao C. and Guo L. PID controller design for second order nonlinear uncertain systems, Science China – Information Sciences, 60(2): 022201, doi: 10.1007/s11432-016-0879-3, 2017.
[14] 郭雷. 不确定性动态系统的估计、控制与博弈. 中国科学: 信息科学, 2020, 50: 1327–1344, doi: 10.1360/SSI-2020-0277, Guo L. Estimation, control, and games of dynamical systems with uncertainty (in Chinese). Sci Sin Inform, 2020, 50: 1327–1344, doi: 10.1360/SSI-2020-0277.
[15] 郭雷. 回溯自校正调节器研究之路.系统科学与数学, 2012, 32(12): 1460-1471.
[16] 郭雷、程代展、冯德兴. 控制理论导论――从基本概念到研究前沿,科学出版社,北京,2005。
[17] Guo L. Feedback and uncertainty: Some basic problems and results, Annual Reviews in Control, Vol.49,pp.27-36, 2020. https:// doi.org/10.1016/j.arcontrol.2020.04.001
本文来源于互联网,e-works本着传播知识、有益学习和研究的目的进行的转载,为网友免费提供,并以尽力标明作者与出处,如有著作权人或出版方提出异议,本站将立即删除。如果您对文章转载有任何疑问请告之我们,以便我们及时纠正。联系方式:editor@e-works.net.cn tel:027-87592219/20/21。