我们知道，描述现实世界物理现象的数学模型大部分是微分方程，而计算机在求解过程中，需要用数学方法将这些微分方程转化为代数方程，进而通过求解代数方程来获得原微分方程的解。那么计算机是如何将微分方程转化为代数方程的呢？这就用到了数值方法。今天，我们就来聊聊CFD数值方法的那些事儿。

引言

    CFD是计算流体力学(Computational Fluid Dynamics)的简称，它从计算方法出发，利用计算机快速的计算能力得到流体控制方程的近似解。求解CFD的数值方法有多种，从有限差分、有限体积、有限元到近年来较为流行的无网格方法，在CFD中都有各自的应用。

回顾：有限体积法

    在CFD领域，有限体积法是常用的一种数值算法。它将流体的控制方程——N-S方程在单元控制体内进行积分后离散求解。由于有限体积法天然地满足质量守恒定律，使流体力学家易于理解，很早就被应用于商业软件中。

探究：有限元法在CFD领域发展滞后的缘由

    有限元法在固体力学中应用广泛，但在CFD领域则发展较为滞后，这是为什么呢？下面我们就来简单介绍一下有限元理论在CFD中的应用。

    与有限差分和有限体积法类似，有限元法求解流体也是从N-S方程开始。但在SUPG/PSPG技术应用于有限元法之前，有限元方法受到很大挑战：一方面有限元的流体应用被稳定性所困扰，另一方面要解决流体力学家很在意的质量守恒问题。究其原因，在于有限元法并不直接对N-S方程进行离散，而是先对其进行积分，利用散度定理和分部积分将N-S方程化为弱积分形式。通过有限单元的划分将连续的积分方程转化为离散的方程组，从而进行速度-压强混合求解。

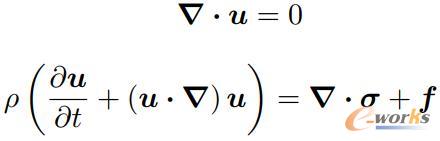
图1 流体控制方程：N-S方程

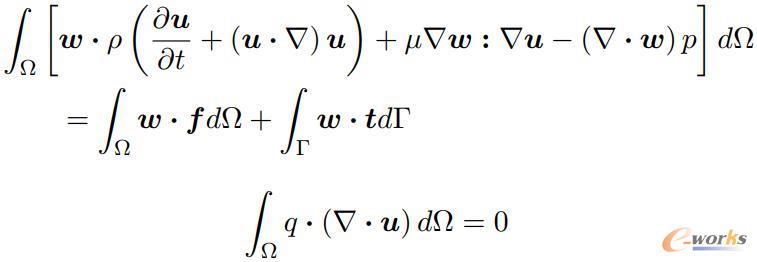
图2 N-S方程的弱积分形式

    但若使用传统的单元(压强和速度插值精度相同)，则会产生不稳定的压强解。另一方面，对于雷诺数较大的情况，也会出现计算结果不收敛。

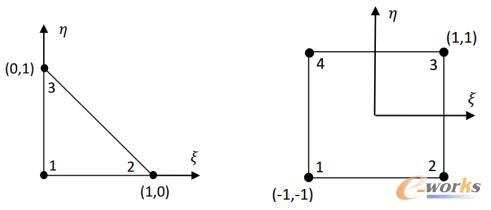
图3 传统等参线性单元

    例如，在经典的lid-driven cavity问题中，当雷诺数Re=100时，采用传统线性单元会得到如图所示的不稳定压强解，速度解则基本正常。而当Re=1000时，计算无法收敛。这主要是由于传统单元不满足一种叫做Ladyzenskaja-Babuska-Brezzi(LBB)的相容性条件，而无法实现速度-压强混合有限元求解的稳定性。

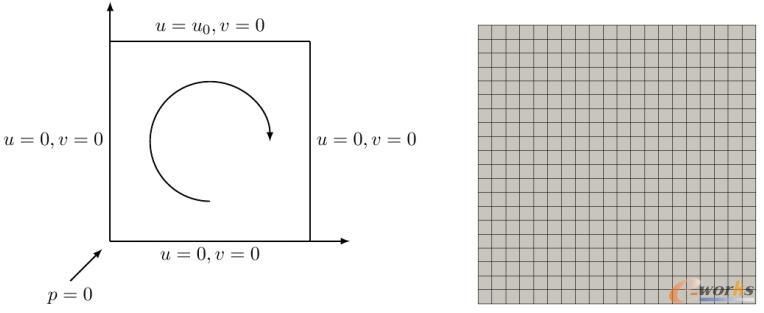
图4 Lid-driven cavity问题：几何与网格

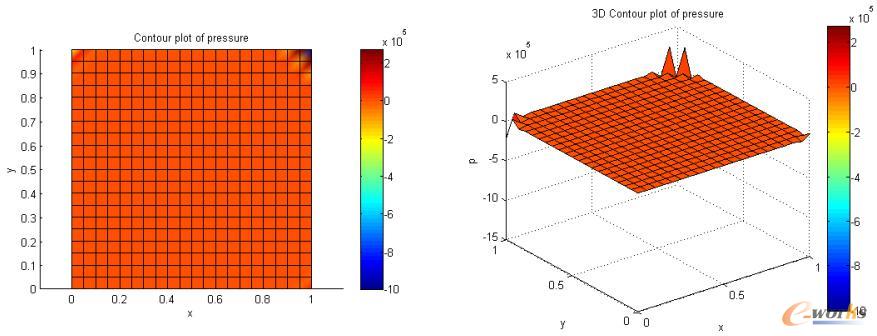
图5 Lid-driven cavity问题：不稳定压强场分布，Re=100

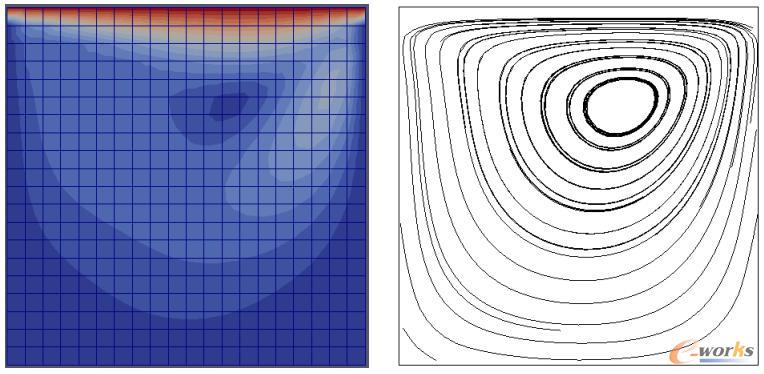
图6 Lid-driven cavity问题：速度场及流线图，Re=100

    解决此问题的方法有两种：一种是采用LBB稳定单元，即速度和压强进行不同阶次的插值，以此满足LBB条件，实现稳定的压强和速度解。但这种方法需要构造特殊的单元形式，较为复杂，同时压强和速度节点数的不同给数据的储存和软件的开发带来困难。

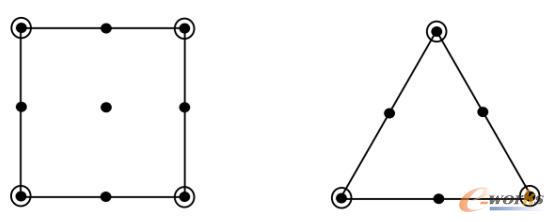
图7 LBB稳定单元(实心点为速度节点，空心点为压强节点)

    另一种方法是对N-S方程的弱积分形式进行修改，增加两个稳定项，SUPG和PSPG项，分别用于处理速度和压强的稳定。在这种情况下，可以采用传统的单元形式，得到稳定的数值解。

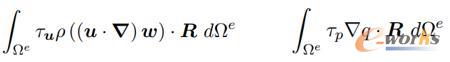
图8 SUPG(左)和PSPG(右)项

    如图，在使用SUPG/PSPG有限元法后，可以得到Lid-driven cavity问题的稳定光滑的压强解，以及较大雷诺数下的数值解。

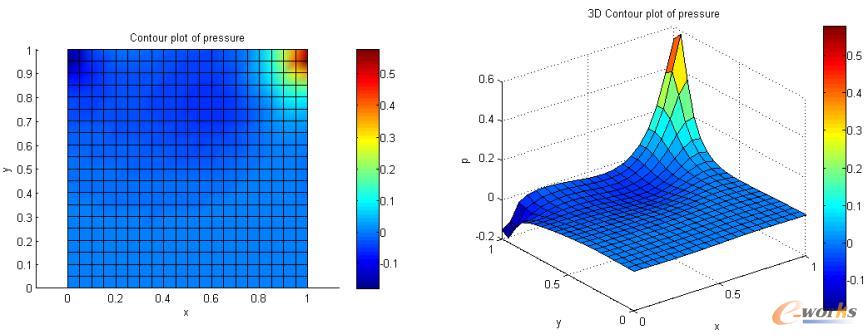
图9 Lid-driven cavity问题：SUPG/PSGP方法得到的压强场分布，Re=100

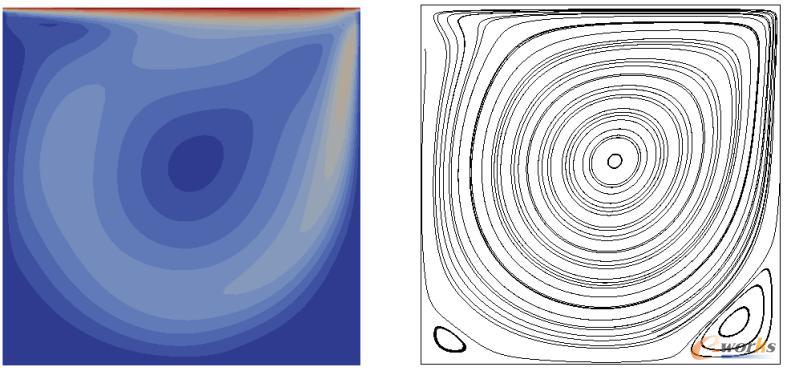
图10 Lid-driven cavity问题：速度场及流线图，Re=1000

    对于经典的圆柱绕流问题，SUPG/PSPG也可以给出较为精确的解。

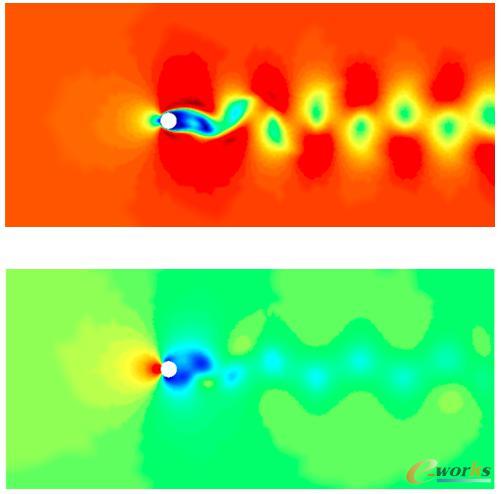
图11 圆柱绕流问题：速度场及压强场分布

    实际上，相对于有限体积法，有限元的精确度、对几何边界处理的灵活性都更为优越。但由于SUPG/PSPG技术在1980年代初才出现，彼时一些使用有限体积法的商业软件早已占领市场，导致有限元至今也没有在CFD中得到广泛应用。

展望：无网格方法发展迅猛

    近年来，随着工程仿真问题的复杂多变，使得上文所介绍的基于网格的传统数值方法在处理某些问题时遇到困难，如涉及到流体边界变形、自由表面流动和多场耦合的问题时，涉及到网格的移动或大变形，往往需要进行网格重构，这使得计算成本大大增加。而无网格方法，具有计算不依赖于网格的天然优势，使其在算法、工程应用及商业软件的开发上都取得了长足的进展，尤其近年来更是发展迅猛。如上海索辰信息科技有限公司推出的通用CFD软件Aries，采用的即是基于分子动力学方法的显示瞬态流体求解器，在计算效率、并行化等方面都具有极大的优势。

    分子动力学方法，将连续介质看作大量离散流体质点粒子。粒子按碰撞和迁移规则运动，通过对各流体质点运动特征的统计，获得流体宏观运动规律，进而得到各物理量，如温度、压力、速度等。Aries采用分子动力学方法，具有高精确性和方便性，突破了高马赫数限制，且优化的求解器在速度和对硬件的资源要求之间达到了很好的平衡。能够解决如低密度、高空稀薄气体气动力学问题等传统基于N-S方程的数值方法不再适用的问题。