一般来说，转子和轴承决定着整台机器的寿命。由于转子的转速不断提高，转子与轴承间的作用力不断增强，从而使振动过载和振动位移增大，寿命降低。转子旋转时，由偏离造成的离心力会使转子产生横向振动，这种振动在临界转速上显得异常强烈。为确保机器在工作转速范围内不致发生共振，临界转速应适当偏离工作转速。尽量避免转子在受到某种激励之后产生的共振给转子带来的严重损坏。传统的转子动力学分析采用传递矩阵方法进行，由于将大量的结构信息简化为极为简单的集中质量——梁模型，不能确保模型的完整性和分析的准确度；而有限元在处理转子动力学问题时，可以很好地兼顾模型的完整性和计算的效率，但多年来转子的“陀螺效应”一直是制约转子动力学有限元分析的“瓶颈”问题。有限元软件ANSYS虽然解决了动力特性分析中“陀螺效应”影响的问题，但是其计算过程需要编写命令流，直观性较差，对于初学者来说，掌握起来比较困难。专业的转子动力特性分析软件SAMCE ROTOR能够较好的解决这些问题，可以极大的提高工作效率。

1 转子系统有限元模型

       从力学角度来看，计算转子临界转速就是求解1个机械系统的特征值。一般来说，1个旋转机械系统的运动微分方程可以写为

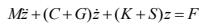
       式中：C为阻尼阵；G为陀螺阵；K为刚度矩阵的对称部分；S为刚度矩阵的不对称部分。

       各矩阵一般都是转速ω的函数。求解这类方程的特征值很困难，特别是当自由度较多时，最常采用传递矩阵法和有限元法。

       采用有限元方法计算转子临界转速时，转子会出现正进动和反进动。由于陀螺效应的作用，随着转子自转角速度的提高，反进动固有频率降低，而正进动固有频率将提高。根据临界转速的定义，应只对正进动固有频率进行分析。在后处理中首先剔除反进动固有频率，然后分析各阶模态模型确定同一阶振型的正进动与反进动固有频率。改变转子自转角速度ω，计算出新的进动角速度Ω，最后画出曲线Ω～ω，即转子坎贝尔曲线。根据临界转速定义，当Ω=ω时，Ω即所求临界转速。

2 利用SAMCE ROTOR计算临界转速及振型分析

       本文采用的SAMCE ROTOR软件支持四种有限元模型，分别为：

       (1)一维模型——由梁、弹簧或者集中质量构建的模型。模型有点和线组成。模型能近似的计算出旋转系统的低阶模态及临界转速，定性的描述旋转体模态及临界转速的变化规律。但对应较复杂的旋转体，其精度略低；

       (2)二维模型——由二维傅立叶谐函数单元构建的模型；

       (3)三维模型——由任意三维实体单元构建的模型；

       (4)混合模型——以上三种转子模型可以同时使用。

       这里所提到的模型包括转子、静子、连接部件。连接部件是指连接转子和固定部件或者连接不同旋转零件的结构，比如滚动轴承、滑动轴承、挤压油膜阻尼器、密封、齿轮等。

       SAMCE ROTOR软件的优势在于它可以直接在转子三维模型的基础上进行转子动力学计算，通过非常直观的操作流程完成分析工作。这不仅提高了计算精度，还简化了分析过程。叶轮、风扇等带有叶片的零件不需要将叶片简化为集中质量，可以直接计算。

       但是当转子较为复杂时，采用三维模型计算规模大，对计算机的要求高，计算时间长。这种情况可以选用二维模型进行计算。二维模型的优势在于计算规模小，计算速度快，能够真实的描述盘、轴等结构，不足之处是不能够真实的描述叶片结构，需要将叶片简化为集中质量施加于轮盘上。通常情况下，选用二维模型结果是可以接受的，但是如果叶片转动惯量很大，就需要用其它方法描述。由于二维模型可以由转子的二维工程图转化而来，因此计算的准备工作较为简便。

       本文采用SAMCE ROTOR软件对某小型涡喷发动机转子系统的临界转速进行了计算，分别采用转子的二维模型和三维模型作为计算数据，分析计算结果并对比两种模型的差异。

       算例分析：某小型涡喷发动机转子系统，如图1所示，由离心叶轮、芯轴、涡轮等零件组成，转子支撑在两个陶瓷轴承上。分别采用二维模型（图3）和三维模型（图4）进行计算，求出了坎贝尔曲线（图2），得到了转子一阶和二阶临界转速及振型（图5～图10），最后对计算模型的大小、计算时间、计算结果进行对比（表1和表2）。

图1 发动机转子三维模型图

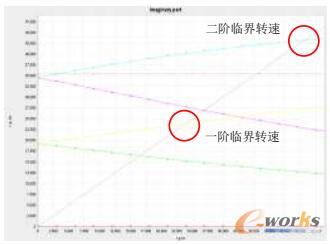
图2 坎贝尔曲线

图3 转子二维计算模型

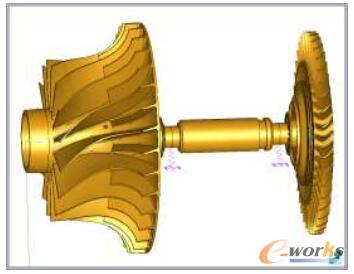
图4 转子三维计算模型

图5 二维模型计算的一阶临界转速

图6 三维模型计算的一阶临界转速

图7 二维模型计算的二阶临界转速

图8 三维模型计算的二阶临界转速

图9 二维模型扩展后的一阶临界转速

图10 二维模型扩展后的二阶临界转速

表1 模型大小和计算时间对比

表2 计算结果对比

       从模型大小和计算时间对比可知，采用二维模型所表示的自由度与三维模型相当，这说明二者对转子结构的描述基本一致，但在节点数和CPU计算时间上，二维模型明显占优，减少了对计算机资源的占用，节省了计算时间。

       从振型可知，第一阶临界转速以转子前部的振动为主，表现为离心叶轮的摆动，第二阶临界转速以转子后部的振动为主，表现为涡轮的摆动。当需要调整第一阶临界转速时，由于该阶临界转速以转子前部振动为主，根据以往的计算经验，对转子前部的结构调整，会对该阶临界转速产生较大的影响。同样，当需要调整第二阶临界转速时，需要对转子后部进行结构调整。转子结构的调整包括零件材料的变化、零件尺寸的变化、轴承位置的变化等。

       从计算结果对比可知，一阶临界转速相差3.7%，二阶临界转速相差8.2%。说明选用二维模型和选用三维模型进行计算所反映的临界转速分布基本一致。如前所述，二维模型将叶片简化为集中质量施加于轮盘上，如果叶片转动惯量很大，采用这种描述方式就会带来一定的误差。转动惯量分为极转动惯量（绕转子转轴）和直径转动惯量（绕轮盘任一直径），本文的算例中，一阶临界转速表现为离心叶轮的摆动，二阶临界转速表现为涡轮的摆动，摆动是直径转动惯量的体现，通过计算，涡轮叶片的直径转动惯量是离心叶轮叶片的5.7倍，由于一阶临界转速主要受离心叶轮的影响，二阶临界转速主要受涡轮的影响，理论上涡轮叶片简化后引起的二阶临界转速误差应该比离心叶轮引起的一阶临界转速误差大。事实上，一阶临界转速相差3.7%，二阶临界转速相差8.2%，也正说明了这一点。

3 结论

       通过转子动力特性分析软件SAMCE ROTOR计算了转子系统的临界转速和振型，并对二维模型和三维计算模型分别进行了计算和对比分析。二者所反映的临界转速分布基本一致，三维模型计算精度高，二维模型计算速度快。因此建议在工程研制初期选用二维模型计算临界转速，便于尽快的对方案进行筛选和调整，避免工作转速达到临界转速产生共振现象。在详细的结构设计完成后，再选用三维模型进行临界转速计算，从而更精确的计算出转子系统的临界转速，通过计算仿真数据为实际试验提供参考和理论依据。