1 引言

    随着机械工业的迅猛发展，计算机仿真分析技术已经在国内外的机械设计领域得到了非常广泛的应用，显著地提高了机械设计水平和效率。有限元分析的基本概念是用较简单的问题代替复杂问题后再求解。将求解域看成是由许多称为有限元的小的互连子域组成，对每一单元假定一个合适的近似解，然后推导求解这个域的满足条件，从而得到问题的近似解。有限元法是目前工程设计领域中使用广泛的现代设计方法，它与传统解法相比更加可靠，具有物理意义直观明确、解题效率高等优点。Altair HyperWorks中的OptiStruct模块是世界领先的基于有限元的优化工具，应用拓扑、外形和形状优化技术，具有强大的功能，帮设计师设计优化出基于各种约束条件下的具有最小重量和最大性能的结构。纵封部由压块、气缸、支架、支撑滚轮等组成，主要功能是对圆柱状的育苗容器无纺布进行加热封装。纵封部支架在整个结构中起固定、支承和安装其余零部件的作用，重量约占整个纵封部的30%，故在满足支架正常工作所需强度和刚度要求的前提下，对纵封部支架进行结构优化设计。

2 有限元模型

    有限元方法就是先将连续的求解域离散为有限个单元体，使其只在有限个指定的节点上相互连结。然后对每个单元选择一个比较简单的函数，近似表达单元的物理量，如单元的应力或位移，并基于问题描述的基本方程建立单元节点的平衡方程组。再把所有单元的方程组集成为整个结构力学特性的整体代数方程组。最后引入边界条件求解代数方程组而获得数值解，如结构的应力分布和位移分部等。在结构的离散化完成后，就可以对典型单元进行特征分析。单元分析的主要目的是建立单元刚度矩阵，根据刚度矩阵便可进一步得出节点力和节点位移的关系：

{F}^e={K}^e{δ}^e

    其中，{F}^e为单元节点力矩阵；{K}^e为单元刚度矩阵；{δ}^e为单元节点位移矩阵。

    利用HyperWorks软件的HyperMesh模块创建支架的有限元网格模型，如图1所示。设定弹性模量E=2.0×10⁵MPa，泊松比μ=0.3。

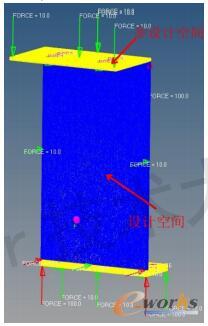
图1 支架的有限元模型

3 支架拓扑优化

    HyperWorks/OptiStruct默认采用正交惩罚材料密度法（SIMP）求解拓扑优化问题，基于SIMP法的结构单工况静态拓扑优化数学模型如下：

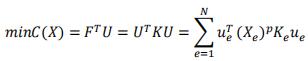
    其中，X是设计区域内的单元相对密度；N是设计区域内节点总数；C是结构整体柔度；F、K、U分别是结构的载荷矩阵、刚度矩阵、位移矩阵；U_e、K_e、u_e分别为单元节点的位移矢量、刚度矢量、单元体积。

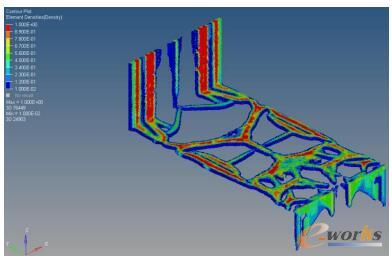
图2 拓扑优化结果云图

    整个过程经历80个迭代步，经过拓扑优化计算后，输出拓扑结果云图，将密度值调到0.15，如图2所示。支架的拓扑优化结构呈工字型结构，对称分布。根据拓扑优化结果的模型，进行结构优化细节设计，结合优化结构的传力路径并考虑铸造工艺特点，调整支架结构得到下图3的优化设计方案。

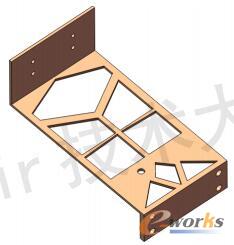
图3 拓扑优化结果模型

4 支架拓扑优化结构强度验证

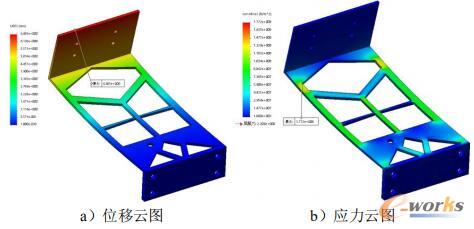
图4 优化结果强度分析

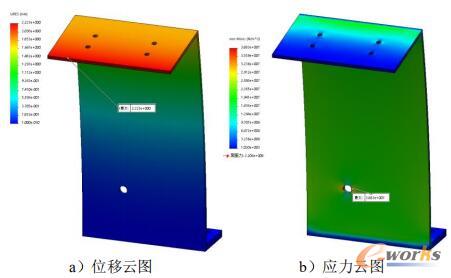
图5 优化前强度分析

    从图4优化位移云图可以看出，最大变形发生在上端面，优化后的最大变形量为6.685mm，而优化前的原始模型最大变形量为2.223mm。优化设计方案是在材料去除32.9%得到的，优化后的实际重量为1.430kg，优化后的体积和位移基本满足要求。

5 结论

    使用HyperWorks对纵封部支架的结构进行拓扑优化，获得新的模型结构。优化前后对比发现，在去除了部份材料的情况下，支架的刚度和强度依然符合要求，验证了该优化结构的正确性。在满足要求的前提下，优化后支架减重0.702kg，减重率为32.9%，取得了一定的轻量化效果。